Постановка задачи проектирования
Для объекта, описываемого уравнениями вида
требуется обеспечить максимальное значение общего коэффициента полезного действия
где
при условии достижения за заданное время требуемого конечного температурного состояния при наличии энергетических и технологических ограничений вида: – удельная поверхностная мощность – максимальный перепад температур по сечению заготовки в период нагрева в области упругих деформаций (на первой стадии нагрева) – – максимальная температура наиболее нагретой точки по сечению заготовки – перепад температур между наиболее нагретой точкой и центром заготовки на выходе – – максимальная индукция в магнитопроводе – температура магнитопровода – ширина паза должна быть больше величины зазора между магнитопроводом и заготовкой Варьируемые параметры 1. Количество пазов (определяет степень неравномерности температур под пазом и зубцом и величину потока рассеяния в пазу); 2. Соотношение ширины 3. Плотность тока в индукторе (j); 4. Параметры футеровки: толщина (s), коэффициент теплопроводности материала футеровки
Обеспечить одну и ту же мощность при удовлетворительных электротепловых режимах работы можно при бесконечно большом числе комбинаций для значений геометрических размеров системы. Однако, геометрия ферромагнитных устройств определяется в основном двумя условиями: во–первых, по требованиям производства, технологии и применения относительные и абсолютные размеры таких устройств должны быть стандартизованы; во-вторых, два геометрических тела, сочлененных между собой, имеют суммарный минимальный объем только при вполне определенных значениях своих линейных размеров. Второе обстоятельство с дополнением ряда электротехнических и конструктивно-технологических ограничений является основой для стандартизации геометрии ферромагнитных устройств [5]. Из физических величин ферромагнитных устройств с геометрией связаны лишь плотность тока и индукция. При этом на геометрию эти величины влияют неоднозначно. При заданных потерях в стали или токе намагничивания максимальное значение индукции достигается при наименьшей средней линии магнитопровода. Увеличение плотности тока с ограничением потерь мощности или напряжения в катушках достигается минимизацией объема обмоточного материала, то есть путем уменьшения сечения и средней длины катушек. Совершенно противоположно влияет геометрия на увеличение индукции и плотности тока при ограничениях по нагреву. Здесь должны быть развитыми поверхности охлаждения, что потребует вариации всех трех относительных размеров. В свою очередь, минимум удельно-экономического показателя достигается только при вполне определенных значениях этих размеров. В связи с изложенным показатели независимой геометрии корректируются в зависимости от того, каким главным критерием должно удовлетворять проектируемое устройство [52, 64, 67]. Методика поисковой процедуры при расчете конструктивных параметров индукционной системы приведена ниже.
1. По известному диаметру заготовки
где δ- величина воздушного зазора; s – толщина футеровки.
2. Определяем количество пазов и зубцов. Исходя из соображений, что
округляем полученное число до ближайшего из ряда Число пазов и зубцов принимаем одинаковым
3. Определяем геометрические размеры паза. Т.к. заранее принимаем, что
Высота паза равна
где
Тогда
Для первоначального расчета принимаем размеры обмотки:
где
4. Внешний диаметр магнитопровода индуктора
5. После определения геометрических параметров системы, создаем геометрическую модель для численного расчета посредством ЭВМ (рис.4.6.). Разбиение основных элементов системы на дополнительные блоки упрощают дальнейший перенос данных между расчетами и никак не влияют на процесс программного решения.
6. Следующим этапом расчета является выделение в рассматриваемой системе блоков и присвоение (задание) соответствующих физических и энергетических параметров. В качестве источников поля для задачи магнитного поля переменных токов выбираем полный ток, для чего задаем амплитудное значение тока и фазовый сдвиг.
Полный ток определяем
где Выбор плотности тока обусловлен ограничениями, определяемыми допустимыми активными потерями мощности. Потери активной мощности в обмотках ограничиваются в основном тремя факторами: — допустимым перегревом катушек; — потерями напряжения в активном сопротивлении обмоток; — оптимальным коэффициентом полезного действия. Каждому из перечисленных факторов соответствуют свои критерии. При оптимальном проектировании следует задаваться одним, а два других рассматривать как контрольные (ограничения).
Рис. 4.6 — Геометрическая модель для расчета системы методом конечных элементов 1 – магнитопровод; 2 – заготовка; 3 – футеровка; 4 – воздушный зазор; 5 – обмотка; 5 – изоляция; 7 – трубка системы охлаждения
7. Задаем граничные условия. 8. Разбиваем исходную модель на сетку конечных элементов. При выборе шага дискретизации (автоматическом или ручном) необходимо учитывать несколько факторов: — временной (с уменьшением шага увеличивается число конечных элементов и соответственно значительно возрастает время расчета); — погрешность (с уменьшением линейных размеров конечных элементов возрастает количество элементов в модели, при этом время вычислений возрастает, а ошибки анализа уменьшаются; но ошибки уменьшаются не до нуля, т. к. с увеличением числа элементов накапливаются ошибки округления в ЭВМ); — программный (при очень больших или очень маленьких шагах дискретизации заложенная в программу процедура решения СЛАУ приводит к тому, что ряды Ньютона не сходится, и дальнейшее решение невозможно). 9. Запускаем процедуру решения задачи. 10. Получаем интегральные и локальные характеристики. 11. Проверяем по условию предельно допустимого значения магнитной индукции в магнитопроводе – 0,8 Тл. Увеличение максимальной рабочей индукции при постоянстве остальных параметров всегда увеличивает мощность устройства и тем самым улучшает удельно-экономические показатели. Естественным ограничением для увеличения индукции является свойство электротехнических сталей насыщаться, после чего индукция почти не меняется. Для устройств индукционного нагрева рабочая индукция должна быть значительно ниже индукции насыщения. Кроме того, ограничение индукции связано также необходимостью ограничения температуры магнитопровода из-за потерь в стали, а иногда – заданного тока намагничивания, заданного коэффициента полезного действия, также во многом зависящих от потерь в стали. В данном случае аналогично выбору плотности тока один из критериев выбирается центральным, другие выступают в роли ограничений. 12. В случае выполнения данного энергетического требования переходим к расчету тепловой задачи. В случае невыполнения требования – снижаем величину плотности тока или изменяем геометрические параметры системы и решаем задачу снова. 13. Для решения тепловой задачи необходимо определить распределение внутренних источников тепловыделения из электромагнитной задачи.
14. Создав геометрическую модель, присвоив физические параметры соответствующим блокам и определив источники тепловыделения, решаем задачу теплопроводности с внутренними источниками тепла для заготовки. Ввиду того, что нагреваемое тело является ферромагнитным, необходимо учитывать переход его через точку магнитных превращений. Но переход осуществляется не мгновенно для всего цилиндра, а растянут во времени, что определяется постепенной потерей магнитных свойств от поверхности к центру по мере увеличения температуры заготовки. Используемый программный пакет не позволяет отразить зависимость магнитной проницаемости среды от температуры, поэтому решение задач производится итерационно, заготовка рассматривается как многослойное тело, по мере прогрева цилиндра пересчитывается распределение внутренних источников тепла и полученные данные переносятся в задачу теплового расчета для заготовки. 15. После получения заданного температурного распределения для нагреваемого ферромагнитного цилиндра решается тепловая задача для нагрева системы «магнитопровод-паз-футеровка», на которую также наложены технологические и энергетические ограничения. Геометрическая модель тепловой задачи полностью повторяет модель электромагнитной задачи, источником тепла является мощность тепловыделения в обмотке, расположенной в каждом пазу магнитопровода. Задаваемые на внешних поверхностях граничные условия позволяют учесть охлаждение с поверхности заготовки. Алгоритм расчета оптимальных параметров индукционного нагревателя представлен на рис. 4.7. После проверки результатов на соответствие накладываемых ограничений решение задачи нагрева для системы «магнитопровод-паз-футеровка» считается законченным. Заключительным этапом расчета является определение интегральных параметров системы – расчет и выбор числа витков и сечения проводов катушки индуктора в соответствии с выбранным напряжением источника питания и расчет системы охлаждения.
Рисунок – 4.7 Алгоритм расчета параметров индукционного нагревателя
|

 ;
; ;
; ;
; ;
; ;
;  ;
; ; (4.1)
; (4.1) ;
; ;
;  ,
, , (4.2)
, (4.2) - электрический КПД:
- электрический КПД:
 ,
, ,
,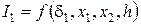 ,
, - тепловой КПД:
- тепловой КПД: ,
,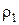 ,
,  - соответственно удельные сопротивления материала катушки индуктора и металла заготовки;
- соответственно удельные сопротивления материала катушки индуктора и металла заготовки; 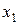 – ширина паза,
– ширина паза,  – ширина зубца,
– ширина зубца,  – высота паза,
– высота паза,
 ;
; ;
; ;
; ;
; ;
; ,
,  ;
; ,
, 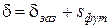 .
. .
. определяем внутренний диаметр индуктора
определяем внутренний диаметр индуктора  :
: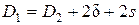 ,
, и
и  , вычисляем
, вычисляем ,
,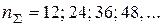 .
. .
. ,
, 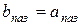 , то
, то .
. ,
, - толщина изоляционного слоя;
- толщина изоляционного слоя; - высота охлаждающей трубки (принимается исходя из расчета охлаждения).
- высота охлаждающей трубки (принимается исходя из расчета охлаждения). .
. ,
, .
. выбирается исходя из обеспечения наименьшего веса, объема и стоимости устройства на единицу мощности, поэтому
выбирается исходя из обеспечения наименьшего веса, объема и стоимости устройства на единицу мощности, поэтому .
. ,
, .
.




