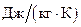Исследование температурных полейв системе «индуктор—заготовка» Тепловая задача формулируется как задача расчета температурного поля (нестационарная теплопередача) [99]. ELCUT позволяет решать задачи теплопередачи (стационарные и нестационарные) в линейной и нелинейной постановках. При решении тепловой задачи использовалось уравнение теплопроводности в виде:
где T – температура; t – время;
q – удельная мощность тепловыделения, задаваемая кубическим сплайном функция температуры;
ρ – плотность. ELCUT позволяет задать источники тепла в блоках, рёбрах или отдельных вершинах модели. Объемная плотность тепловыделения, заданная для блока модели, соответствует объемному источнику тепла. Следующие виды граничных условий могут быть заданы на внешних и внутренних границах расчетной области. Условие заданной температуры(ГУ I рода)задает на ребре или в вершине модели известное значение температуры Условие заданного теплового потока(ГУ II рода)описывается следующими соотношениями:
где Для внутренней границы Если мощность тепловыделения задана на внешнем ребре, являющемся следом плоскости симметрии задачи, истинное значение мощности тепловыделения следует разделить пополам. Граничное условие конвекции (ГУ III рода) может быть задано на внешней границе модели. Оно описывает конвективный теплообмен и определяется следующим образом:
где α - коэффициент теплоотдачи, и Параметры α и Граничное условие радиации может быть задано на внешней границе модели. Оно описывает радиационный теплообмен и определяется следующим образом:
где Чтобы задача расчета температурного поля была поставлена корректно, необходимо поставить хотя бы в одной вершине условие заданной температуры, либо хотя бы на одном ребре условие конвекции или радиации. Граничное условие равной температурыможет быть использовано для описания тел с очень высокой, по сравнению окружающими телами, теплопроводностью. Внутренность такого тела может быть исключена из расчета температурного поля, при условии описания всей его поверхности как поверхности равной температуры. Данное условие отличается от условия первого рода тем, что температура на описываемой поверхности неизвестна заранее. Ребро, описанное условием равной температуры, не должно соприкасаться с любым ребром, где температура задана явно. В последнем случае ребро с условием равной температуры должно быть переопределено при помощи граничного условия первого рода с подходящим значением температуры. При анализе результатов задачи ELCUT позволяет оперировать со следующими локальными и интегральными физическими величинами. Локальные величины: · Температура T; · Вектор плотности теплового потока
Интегральные величины: · Поток тепла через заданную поверхность
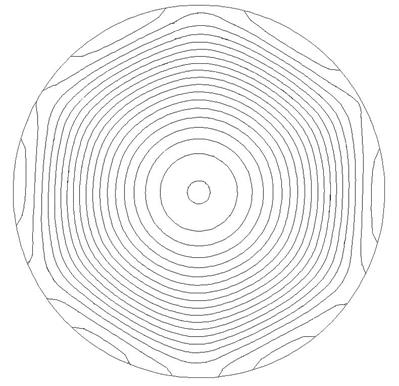
где n - единичный вектор нормали к поверхности. Поверхность интегрирования задается контуром в плоскости модели, состоящим из отрезков и дуг окружностей. Тепловая задача для заготовки представляет собой нелинейную задачу нестационарной теплопередачи. Геометрическая модель заготовки выбрана плоской и соответствует геометрии электромагнитной задачи. Разбиение на блоки производилось таким образом, чтобы максимально реально возможно было перенести данные из электромагнитной задачи (толщина колец выбиралась соответствующей глубине проникновения тока, радиальное деление осуществлялось из условия разной величины тепловыделения под пазами индуктора и под зубцами). Исходные данные сведены в таблицу 3.6. В качестве источников тепла задавалась объемная плотность тепловыделения, что соответствует объемным источникам тепла внутри каждого блока. В качестве граничного условия на поверхности заготовки задавалась радиация с коэффициентом поглощения поверхности Шаг интегрирования составил 1 секунду. Обозначения «п» и «з» соответствуют областям под пазом и под зубцом. Наглядное представление результатов решения задачи представлено на рисунках. Неравномерность температурного распределения по окружности заготовки (рис. 3.14) наблюдается только на расстоянии от поверхности, соответствующем глубине проникновения тока в металл. С приближением к центру изотермы принимают вид концентрических окружностей с центром, совпадающим с осью симметрии заготовки [49].
Рисунок 3.14 — Изотермы теплового поля заготовки
Рисунок 3.15 — Распределение температуры в процессе нагрева
Таблица 3.6 — Исходные данные для исследования тепловых полей в заготовке
Рисунок 3.16 — Распределение температуры по контуру поверхности заготовки
Характер кривой распределения температуры по контуру поверхности заготовки (рис. 3.16) соответствует характеру распределения источников внутреннего тепловыделения, приведенному на рис. 3.10, и объясняется различной мощностью нагрева под индуктирующим проводом и под зубцом магнитопровода [71].
Рисунок 3.17 — Температурное распределение по радиальной координате
Рисунок 3.18 — Распределение теплового потока для контура по радиусу заготовки под пазом
График, представленный на рис. 3.18, показывает характер распределения теплового потока. Максимум потока приходится на расстояние примерно 8 - 10 мм от поверхности заготовки. Это объясняется тепловыми потерями с поверхности заготовки [74]. Тепловая задача для магнитопровода представляет собой нелинейную задачу нестационарной теплопередачи. В качестве источников тепла задавалась объемная плотность тепловыделения для медных трубок, разбитых на блоки в соответствии с физикой процесса, переносимая из электромагнитной задачи. Геометрическая модель представлена на рис. 3.19. Для возможности задания граничных условий, отражающих охлаждение, в статоре вычерчивались небольшие разрезы по толщине в области трубок, чтобы искусственно создать внешние границы.
Рисунок 3.19 — Геометрическая модель с сеткой конечных элементов
Исходные данные сведены с таблицу 3.7.
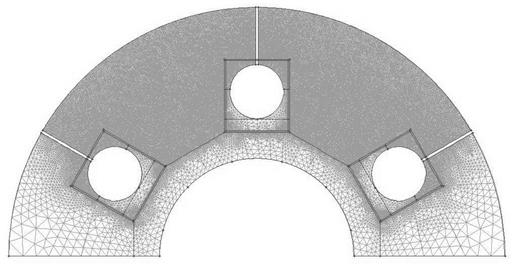
При принудительном охлаждении катушки индуктора и футеровки, температура наружной поверхности футеровки составляет 256°С, температура изоляции катушки — 90°С, что обеспечивает нормальную долгую эксплуатацию установки.
Таблица 3.7 — Исходные данные для исследования тепловых процессов в системе «магнитопровод — обмотка — футеровка»
Рисунок 3.20 — Температурное поле
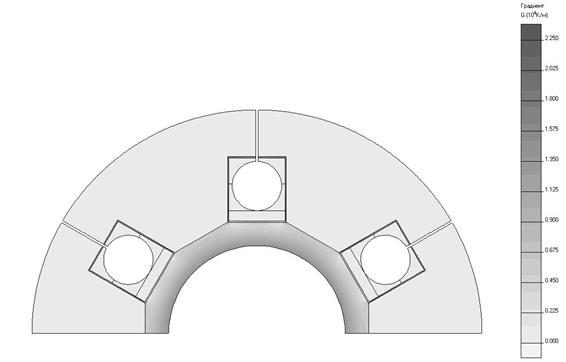
Рисунок 3.21 — Распределение градиента температуры
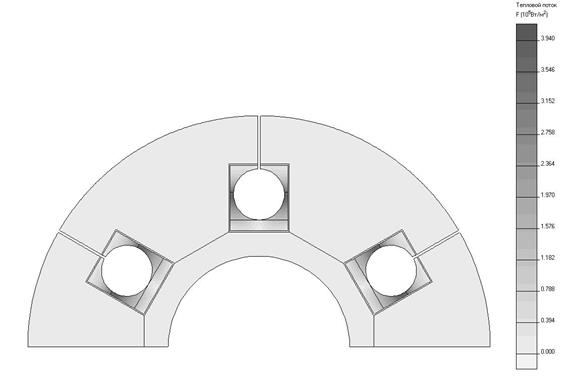
Рисунок 3.22 – Распределение теплового потока
Результаты численных экспериментов показывают, что при использовании принудительного охлаждения катушки индуктора и магнитопровода температурный режим элементов индуктора обеспечивает надежное функционирование установки [75, 53].
Выводы 1. Разработана методика последовательного расчета задач теплопроводности с обменом информацией в виде аппроксимирующих выражений для распределений температуры и магнитной проницаемости. 2. Выполнен расчет и проведен анализ электрических и тепловых параметров элементов индукционного нагревателя и заготовки. Показано, что наибольшее влияние на параметры процесса оказывает соотношение размеров паза и зубца магнитопровода, толщина футеровки и её теплофизические характеристики. 3. Предложена методика расчета электромагнитных и тепловых полей в заготовке и в элементах индукционной системы, позволяющая учесть влияние геометрических и электрофизических параметров элементов индукционной системы на эффективность процесса нагрева.
|
,
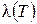– теплопроводность как функция температуры, представленная кубическим сплайном (анизотропия не поддерживается в нелинейной постановке);
- удельная теплоемкость, задаваемая кубическим сплайном функция температуры;
. Значение 
- на внешних границах,
- на внутренних границах,
- нормальная компонента вектора плотности теплового потока, индексы "+" и "−" означают «слева от границы» и «справа от границы» соответственно.
означает поверхностную мощность источника, для внешней - известное значение теплового потока через границу. Если 
,
- температура окружающей среды.
,
- константа Стефана-Больцмана, β - коэффициент поглощения поверхности, и 
, 
- в плоском случае.
,
и начальной температурой 293 К.
