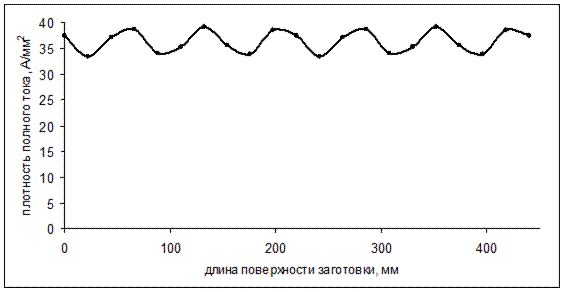
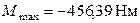Исследование электромагнитных полейв системе «индуктор—заготовка» Для решения электромагнитной задачи выбран тип задачи магнитного поля переменных токов. Анализ магнитного поля переменных токов состоит в расчете электрического и магнитного поля, возбужденного приложенными переменными (синусоидально изменяющимися во времени) токами или внешним переменным полем [54,58]. Представление гармонически изменяющейся величины при помощи комплексного числа существенно облегчает анализ. Действительная и мнимая части комплексного числа
сдвинуты по фазе на 90 градусов по отношению друг к другу, так что их линейная комбинация может представлять произвольный фазовый угол. В зависимости от фазового сдвига между двумя осциллирующими компонентами вектора, вектор может вращаться по часовой стрелке или в противоположном направлении, либо колебаться вдоль некоторого направления. В общем случае конец вектора описывает эллипс. Главные полуоси эллипса соответствуют максимальным значениям векторной величины. Отношение длин меньшей и большей полуосей определяет коэффициент поляризации вектора. Последний предполагается положительным при вращении вектора против часовой стрелки и отрицательным в противоположном случае. Нулевой коэффициент соответствует линейной поляризации вектора. Задача формулируется как дифференциальное уравнение в частных производных относительно комплексной амплитуды векторного магнитного потенциала A (
где электропроводность g и компоненты тензора магнитной проницаемости Источники поля могут быть заданы в блоках, на рёбрах или в отдельных вершинах модели. Источники поля могут включать объемную, поверхностную или линейную плотность тока, а также напряжение, приложенное к проводникам. Пространственно распределенный ток можно задать несколькими способами. В массивном проводнике можно определить либо полный ток, либо напряжение, приложенное к проводнику [99]. Различные блоки модели, в которых задано одно и то же значение полного тока или приложенного напряжения, могут рассматриваться как соединенные последовательно. В этом случае в каждом проводнике протекает один и тот же полный ток, а напряжение, если оно задано, трактуется как приложенное к зажимам всей группы последовательно соединенных проводников. В решаемой задаче в качестве источников поля был задан полный ток в каждом из проводников, уложенных в пазы магнитопровода, с помощью величины амплитуды тока На внешних границах расчетной области задано граничное условие – условие Дирихле. Условие Дирихле задает известное значение векторного магнитного потенциала Параметры a, b и c постоянны для каждого ребра, но могут изменяться от одного ребра к другому. Этот подход позволяет моделировать внешнее однородное поле путем задания ненулевой нормальной компоненты магнитной индукции на любом прямолинейном отрезке границы. Для решаемой задачи было выбрано При анализе результатов расчета магнитного поля переменных токов ELCUT позволяет оперировать со следующими локальными и интегральными физическими величинами. Рассмотрим интегральные величины для блока заготовки (таблица 3.5). Вектор вращающего момента параллелен оси z в плоской постановке. Момент вычисляется относительно начала координат. Магнитное поле порождает силы, действующие на проводники с током и ферромагнитные тела. Сила, действующая на проводники известна под названием силы Лоренца, в то время как сила, вычисленная путем интегрирования тензора Максвелла, включает в себя обе компоненты (полная магнитная сила). Локальные величины (значение которых определяются в конкретной точке): · Комплексная амплитуда векторного магнитного потенциала A; · Комплексная амплитуда напряжения U, приложенного к проводнику; · Комплексная амплитуда плотности полного тока
плотности стороннего тока
· Комплексный вектор магнитной индукции
· Комплексный вектор напряженности магнитного поля
· Среднее и максимальное значение удельной мощности тепловыделения
· Среднее и максимальное значение плотности энергии магнитного поля
· Среднее значение вектора Пойнтинга (плотность потока энергии)
· Среднее значение вектора плотности силы Лоренца
· Магнитная проницаемость μ; · Электрическая проводимость g.
Таблица 3.5 – Интегральные величины для блока заготовки
Рисунок 3.4 — Среднеквадратичные значения индукции
Рисунок 3.5 — Действующие значение плотности полного тока
Рисунок 3.6 — Среднее значение вектора Пойнтинга
Рисунок 3.7 — График распределения плотности полного тока
Рис. 3.8 — График распределения мощности тепловыделения
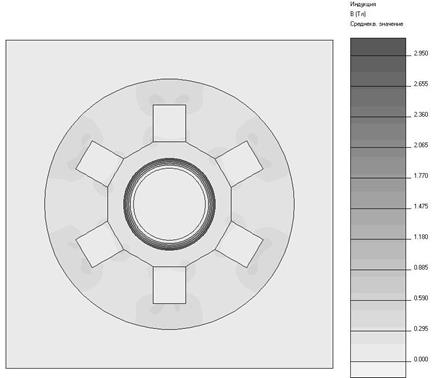
Рисунок 3.9 — График распределения плотности полного тока по контуру поверхности заготовки
Рисунок 3.10 — График распределения тепловыделения по контуру поверхности заготовки
Рисунок 3.11 — График распределения плотности полного тока по высоте паза
Рисунок 3.12 — График распределения тепловыделения по контуру высоты паза
Рисунок 3.13 — Распределения плотности полного тока по радиусу заготовки
|
,
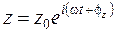, B - вектор магнитной индукции). Вектор магнитной индукции предполагается лежащим в плоскости модели xy, в то время как вектор плотности электрического тока j и векторный магнитный потенциал A ортогональны к нему. Только компоненты 
и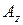 
в плоской постановке и отличны от нуля.
,
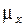и 
постоянны в переделах каждого блока модели. Сторонняя составляющая тока 
предполагается постоянной в пределах каждого блока модели.
и сдвига в 120° между соседними фазами для образования трехфазной системы.
в вершинах или на рёбрах модели. Это условие определяет нормальную компоненту вектора магнитной индукции. Зачастую это условие используется для задания отсутствия нормальной составляющей индукции, например, на оси симметрии или на удаленных границах области. ELCUT также поддерживает условие Дирихле в функции координат по следующей формуле 
.
, т.е. затухание электромагнитной волны на удаленной внешней границе.
,
и плотности вихревого тока
;
, 
;
;
;
;
;
;
; 
; 
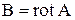
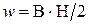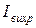
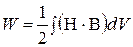
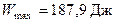
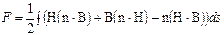
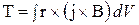где r -радиус-вектор точки интегрирования.
,
где r -радиус-вектор точки интегрирования.
