Математическая модель тепловых процессов
Индукционная система с магнитопроводом, катушками индукторов, футеровкой и цилиндрической загрузкой (рис.2.3) представляет собой сложную комбинацию процессов теплообмена, включающую теплопроводность в твердых телах, теплопроводность через стенку, теплообмен конвекцией и излучением между футеровкой и загрузкой, а также между загрузкой и внешней средой на торцах. Некоторые параметры, как, например, термическое сопротивление в местах контакта разных элементов, сложно определить. В этом случае используются эмпирические усредненные значения. Учитывая имеющуюся периодичность конструкции, обусловленную чередованием пазов и зубцов магнитной системы, исходную математическую модель нестационарной теплопроводности для объекта составной структуры можно представить системой дифференциальных уравнений в частных производных вида:
соответственно для цилиндрической заготовки (2.40), футеровки (2.41) и магнитной системы индуктора (2.42). Теплообмен между боковой поверхностью цилиндрической загрузки содержит две составляющие: конвекцию и излучение. Формулировка граничных условий требует некоторых допущений. В частности, для упрощения можно принять, что отсутствует движение воздуха вдоль направляющей боковой поверхности, что означает циркуляцию воздуха внутри пространства между двумя поверхностями – загрузки и футеровки. Тогда можно с некоторой погрешностью принять для конвективного теплообмена между поверхностями прямую связь без участия воздушной среды.
Рисунок 2.3 — Эскиз индуктора
В этом случае конечное выражение для граничного условия на боковой поверхности цилиндрической заготовки примет вид:
на торцевых поверхностях заготовки
на торцевых поверхностях футеровки
Теплообмен между внешней поверхностью футеровки и индуктором принимается непосредственным, то есть с идеальным тепловым контактом. Граничные условия четвертого рода представляют комбинацию двух уравнений
Граничные условия на внешней поверхности магнитопровода
и на торцевых поверхностях
Здесь
При исследовании температурных полей принимается ряд допущений. 1. Футеровка представляет собой полый цилиндр, изготовленный из материала с низкой теплопроводностью. В связи с этим температурное распределение в стенке футеровки в установившемся режиме можно считать не зависящим от угловой координаты 2. Магнитопровод индуктора можно представить как полый цилиндр с двумя источниками тепла – в виде локальных теплоисточников, обусловленных тепловыделением в индуктирующем проводе, расположенном в пазах магнитопровода, и в виде теплового потока с поверхности заготовки. 3. Проводник в пазу магнитопровода можно считать теплотехнически тонким телом. Особенностью построения численных методов, таких, как метод конечных элементов или метод конечных разностей, является стремление упростить первоначальную формулировку, что обеспечивает существенное снижение сложности преобразований. Решение тепловой задачи выполнено методом конечных элементов (МКЭ), который дает возможность достаточно точно учитывать все нелинейности путем изменения всех нелинейных величин с каждым шагом по времени, а также задать сложную геометрию нагреваемого изделия. При построении конечно—элементной модели такие сложные процессы, как теплообмен на границе двух твердых тел, заменяются комбинацией соседних элементов с различными свойствами. Более сложной является ситуация с теплообменом (конвекцией или излучением) между телами, разделенными воздушной средой. Чаще всего приходится упрощать постановку задачи. В отличие от программы ANSYS программа ELCUT не имеет встроенной процедуры расчета таких процессов. Поэтому во всех сложных случаях была произведена замена теплообмена между телами на теплообмен с окружающей средой с соответствующими расчетами коэффициентов теплообмена. Определение температурного поля нагреваемого изделия сводится к решению уравнения теплопроводности Фурье с известной функцией распределения внутренних источников тепла, найденной в результате решения электромагнитной задачи. Рассмотрим более общую постановку тепловой задачи для трехмерного случая, на базе которой построим конечно—элементную формулировку. Переход к более простым случаям реализуется с помощью упрощений. Первый закон термодинамики для объёмных тел записывается в виде дифференциальных уравнений [31, 95]
где с- удельная теплоёмкость; Т - температура;
Закон Фурье устанавливает связь между вектором теплового потока и температурным градиентом [38, 9]:
где
Объединение уравнений (2.49), (2.50) даст уравнение вида:
Представим уравнение (2.51) в наиболее знакомой форме:
Полученные уравнения будут использоваться для решения задач в декартовой системе координат. Запишем три вида граничных условий: 1. Задана температура, действующая по поверхности:
2. Определяется тепловой поток
где 3. Определяется конвективный теплообмен между поверхностями (закон охлаждения Ньютона):
где
Объединяя уравнения (2.49) с уравнениями (2.54) и (2.55), получим:
Дальнейшие преобразования можно осуществить двумя способами – с помощью метода Галеркина или вариационного исчисления. Различные конечно—элементные реализации расчета полевых задач используют одинаково часто оба этих подхода, так как они приводят к одному результату. Используем вариационное исчисление для преобразования основного дифференциального уравнения (2.52) и граничных условий (2.53), (2.54), (2.55) в энергетический функционал, минимизация которого позволит согласовать внутренние и внешние тепловые потоки с распределением температуры в объеме нагреваемого тела в динамическом режиме.
где V - объём элемента; Запишем (2.58) без явного выражения функционала
= Как видно из ранее записанных выражений, рассматривается линейная постановка задачи. Такой подход позволяет перейти к конечно—элементной формулировке гораздо проще, чем при нелинейной постановке. В методе конечных элементов вся расчетная область покрывается сеткой геометрических элементов. Первоначально для двумерных задач использовались обычные треугольники с узлами в вершинах. В дальнейшем с развитием теории МКЭ были разработаны более сложные формы, такие, как треугольники с шестью узлами, четырехугольники с четырьмя и восемью узлами, а также криволинейные треугольники и четырехугольники. Все это позволило более точно описывать криволинейные границы, повышать точность расчетов без увеличения размерности системы уравнений. Дальнейшая стратегия преобразований заключается в составлении на основании (2.59) выражений для отдельных его составляющих для каждого элемента. Полученные уравнения объединяются в систему дифференциальных уравнений, решение которой дает значения температуры в узлах треугольников на расчетной области. Связь между температурой в узлах и произвольных точках внутри рассматриваемого треугольника определяется зависимостью
где
Для производной температуры по времени запишем выражение
Вариация температуры
Для записи
где
Теперь измененное состояние уравнения (2.62) можно объединить с выражениями (2.61) и (2.63)
Как уже отмечалось, прагматичный подход при построении конечно—элементной модели опирается на представление нелинейного объекта в виде комбинации элементов с неизменными параметрами в пределах отдельных элементов. Все это позволяет упростить преобразования. Наконец,
Выражение (2.65) может быть записано иначе
где
Для удобства составления матриц коэффициентов производится объединение матрицы теплоемкости и составляющей матрицы жесткости, обусловленной движением тела. Их связывает то, что они стоят перед первыми производными температуры (по времени и по продольной координате). Это позволяет организовать идентичный метод расчета через их замену разностным аналогом и последующее интегрирование. Расчет выражений для матриц жесткости и демпфирования, а также векторов источников можно осуществлять либо численно, либо с помощью специальной процедуры аналитического интегрирования в локальных координатах [32]. Исследования показывают, что второй путь дает очень большой выигрыш в общем времени расчета задачи. В большинстве программных продуктов используется именно этот метод. Полученные выражения для элементных матриц объединяются в глобальную систему обыкновенных дифференциальных уравнений (2.64), решение которой осуществляется путем перехода к дискретному аналогу дифференциального уравнения. Полученные матрицы
где Последнее выражение переписывается в виде:
Метод решения системы дифференциальных уравнений выбирается исходя из размерности задачи, а также свойств матриц жесткости. В самом простом случае, когда число узлов невелико, и ширина матрицы небольшая, используются прямые методы, например, Холецкого, Гаусса. Для больших систем прямые методы дают большую погрешность, поэтому применяются итерационные. Выбор метода решения зачастую обусловлен проблемой экономии памяти, возникающей при разбиении расчетной области на элементы. Большое количество элементов повышает устойчивость и улучшает сходимость вычислительного процесса. Однако, это сопровождается увеличением размеров массивов и требуемой оперативной памяти. Соответственно возрастает время счета. Для решения проблемы применяются конечные элементы более высоких порядков, что позволяет обеспечивать нелинейные законы изменения функции между узлами внутри элемента. Тем не менее, иногда для ускорения процесса вычисления приходится увеличивать допустимую погрешность, чтобы получить приемлемое число итераций и общее время счета. Общее уравнение первого порядка с нулевой правой частью f может быть решено численно с помощью двухслойной схемы, записываемой в виде
Если
то в общем случае имеем
Подставив эти выражения в (2.68), получим
В случае положительно определенных матриц К и С все собственные значения
т.е., если
Это условие должно быть выполнено для устойчивости схем интегрирования по времени. Кроме того, схема будет свободна от колебаний, если каждая входящая в виде множителя в
Следовательно, двухслойная по времени схема (2.72) будет устойчива и свободна от колебаний, если
Полученное условие можно ввести в программу как ограничение на максимальный размер шага по времени. Недостатком является то, что нелинейность задачи предопределяет изменение во времени параметров матриц жесткости К и демпфирования С,что приводит к необходимости пересчитывать собственные числа для всего массива элементных матриц, что резко увеличивает общее время расчета задачи. Геометрическая модель загрузки выбрана плоской и соответствует геометрии электромагнитной задачи. Разбиение на блоки производилось таким образом, чтобы было возможно максимально точно перенести данные из электромагнитной задачи (толщина колец выбиралась соответствующей глубине проникновения тока, радиальное деление осуществлялось из условия разной величины тепловыделения под пазами индуктора и под зубцами). В качестве источников тепла задавалась объемная плотность тепловыделения для каждого блока, что соответствует объемным источникам тепла внутри каждого блока. В качестве граничного условия на поверхности заготовки задавалась радиация с соответствующим коэффициентом.
Выводы 1. Сформулирована задача идентификации и предложена численная математическая модель нестационарной теплопроводности в системе, состоящей из цилиндрического индуктора с замкнутым магнитопроводом, во внутренней полости которого расположена цилиндрическая заготовка. 2. Разработана конечно—элементная модель взаимосвязанных электромагнитного и теплового полей в системе «цилиндрический индуктор – заготовка». Разработанная модель позволяет провести расчеты и выполнить анализ распределения мощности электромагнитных источников тепла и температурных полей в цилиндрической заготовке и элементах индуктора.
|



 , (2.40)
, (2.40)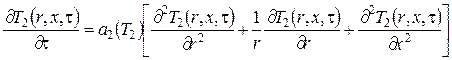 ,
, , (2.41)
, (2.41)
 ,
, . (2.42)
. (2.42)

 , (2.43)
, (2.43)
 , (2.44)
, (2.44)
 . (2.45)
. (2.45) ; (2.46)
; (2.46) . (2.47)
. (2.47)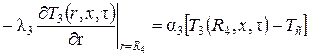
 . (2.48)
. (2.48) ,
,  ,
,  – температурные распределения соответственно в цилиндрической заготовке, футеровке и магнитопроводе индуктора,
– температурные распределения соответственно в цилиндрической заготовке, футеровке и магнитопроводе индуктора,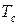 – температура воздуха,
– температура воздуха,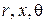 - радиальная, аксиальная и угловая координаты системы,
- радиальная, аксиальная и угловая координаты системы,  – время процесса,
– время процесса, ,
,  ,
,  ,
,  ,
,  ,
,  – коэффициенты температуропроводности и теплопроводности материалов заготовки, футеровки и магнитопровода соответственно,
– коэффициенты температуропроводности и теплопроводности материалов заготовки, футеровки и магнитопровода соответственно, ,
, 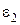 – степень черноты материала загрузки,
– степень черноты материала загрузки, – коэффициент теплообмена внешней поверхности магнитопровода с окружающей средой,
– коэффициент теплообмена внешней поверхности магнитопровода с окружающей средой,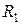 ,
,  ,
,  ,
,  – соответствующие радиусы поверхности заготовки, внутренней поверхности футеровки, поверхности сопряжения футеровки и индуктора и внешней поверхности магнитопровода индуктора,
– соответствующие радиусы поверхности заготовки, внутренней поверхности футеровки, поверхности сопряжения футеровки и индуктора и внешней поверхности магнитопровода индуктора,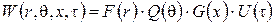 – источники внутреннего тепловыделения в нагреваемой заготовке,
– источники внутреннего тепловыделения в нагреваемой заготовке, – функция распределения источников тепловыделения в индукторе.
– функция распределения источников тепловыделения в индукторе. .
. , (2.49)
, (2.49) плотность;
плотность; - векторный оператор;
- векторный оператор; - вектор теплового потока;
- вектор теплового потока; скорость образования тепла в конечном объёме.
скорость образования тепла в конечном объёме. (2.50)
(2.50) матрица теплопроводности;
матрица теплопроводности; коэффициенты теплопроводности в элементе по направлениям x, y, z соответственно.
коэффициенты теплопроводности в элементе по направлениям x, y, z соответственно. . (2.51)
. (2.51) . (2.52)
. (2.52) (2.53)
(2.53)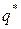 , действующий по поверхности S2
, действующий по поверхности S2 (2.54)
(2.54) - единичный вектор, направленный от поверхности по нормали.
- единичный вектор, направленный от поверхности по нормали. (2.55)
(2.55) коэффициент указанный для элементов
коэффициент указанный для элементов внешняя температура;
внешняя температура; температура на поверхности тела;
температура на поверхности тела; ; (2.56)
; (2.56)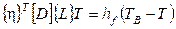 . (2.57)
. (2.57)
 (2.58)
(2.58) вариация температур;
вариация температур;
 . (2.59)
. (2.59) , (2.60)
, (2.60) – температура;
– температура;  – матрица базисных функций;
– матрица базисных функций;  = вектор температуры в узлах элемента.
= вектор температуры в узлах элемента.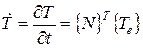 . (2.61)
. (2.61) имеет ту же форму, что и Т
имеет ту же форму, что и Т . (2.62)
. (2.62) используется матричная форма, более удобная для дальнейших преобразований и содержащая продифференцированные выражения от матрицы базисных функций, что исключает необходимость записи в виде производных по координате:
используется матричная форма, более удобная для дальнейших преобразований и содержащая продифференцированные выражения от матрицы базисных функций, что исключает необходимость записи в виде производных по координате: , (2.63)
, (2.63) .
.

 . (2.64)
. (2.64) - являются независимыми от координаты величинами и не изменяются за пределами элемента. С учетом сказанного ряд величин может быть вынесен за знак интегралов. Таким образом, уравнение (2.64) может быть преобразовано к виду:
- являются независимыми от координаты величинами и не изменяются за пределами элемента. С учетом сказанного ряд величин может быть вынесен за знак интегралов. Таким образом, уравнение (2.64) может быть преобразовано к виду:

 . (2.65)
. (2.65) , (2.66)
, (2.66)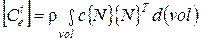 — элементная матрица теплоемкости или матрица демпфирования;
— элементная матрица теплоемкости или матрица демпфирования; — составляющая элементной матрицы жесткости, обусловленная передачей тепла за счет перемещения нагреваемого тела;
— составляющая элементной матрицы жесткости, обусловленная передачей тепла за счет перемещения нагреваемого тела; — составляющая элементной матрицы теплопроводности или матрицы жесткости,
— составляющая элементной матрицы теплопроводности или матрицы жесткости, — составляющая элементной матрицы теплопроводности, учитывающая теплообмен элементов, находящихся на границе области;
— составляющая элементной матрицы теплопроводности, учитывающая теплообмен элементов, находящихся на границе области; — элементный вектор поверхностных источников тепла в виде потока;
— элементный вектор поверхностных источников тепла в виде потока; — элементный вектор теплового потока с поверхности элемента в окружающее пространство путем конвекции;
— элементный вектор теплового потока с поверхности элемента в окружающее пространство путем конвекции; — элементный вектор внутренних источников тепла.
— элементный вектор внутренних источников тепла. ,
,  и
и 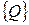 с учетом замены временной производной
с учетом замены временной производной  конечно-разностным аналогом, объединяются в систему уравнений.
конечно-разностным аналогом, объединяются в систему уравнений. , (2.67)
, (2.67) – временной шаг, n – номер шага,
– временной шаг, n – номер шага,  - коэффициент, принимающий значения от 0 до 1.
- коэффициент, принимающий значения от 0 до 1. . (2.68)
. (2.68) (2.69)
(2.69) - собственные значения, а
- собственные значения, а  соответствующие векторы задачи на собственные значения
соответствующие векторы задачи на собственные значения , (2.70)
, (2.70)
 . (2.71)
. (2.71)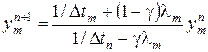 . (2.72)
. (2.72) ,
, 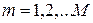 , (2.73)
, (2.73)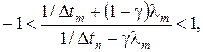
 мода имеет один и тот же знак на всех временных слоях n. В силу равенства (2.71) это будет выполняться, если
мода имеет один и тот же знак на всех временных слоях n. В силу равенства (2.71) это будет выполняться, если




