Процессов индукционного нагрева
Для нагрева изделий в технологических линиях горячей обработки металла на деформирующем оборудовании могут применяться, в зависимости от формы и размеров нагреваемого объекта, а также от организации производственного процесса, различные типы нагревательных установок: пламенные печи, установки кондукционного нагрева, печи сопротивления, установки индукционного нагрева. Последние имеют ряд значительных преимуществ: высокая энергоэффективность, высокая надежность установок и их экологичность, безопасность, возможности широкого и более точного регулирования распределения температур по объему и во времени, минимальные тепловые потери, возможности достижения высоких температур за меньшее время. Совокупность этих факторов делает индукционный нагрев наиболее перспективным и актуальным направлением развития электротехнологии в настоящее время. В то же время индукционный нагрев является одним из наиболее сложных электротермических процессов и в строгой постановке требует рассмотрения взаимосвязанных явлений разной физической природы. Основными процессами являются электромагнитные и тепловые, причем тепловые процессы включают в себя процессы теплопередачи внутри нагреваемого тела и внешнего теплообмена, в том числе теплообмена с охлаждающей средой при термообработке. Поэтому при разработке индукционной системы нагрева проводится последовательное решение задач моделирования электромагнитного и теплового полей; выбора оптимальной конструкции; оптимизации по заданным критериям, а также отработка методики и рекомендации к проектированию с учётом ограничений, накладываемых технологическим процессом. Вопросам теории и методам расчета электромагнитных и тепловых полей при индукционном нагреве посвящены работы В.П. Вологодина, Л.Р. Неймана, Г.И. Бабата, Н.Н. Родигина, А.Е. Слухоцкого, А.В. Донского, А.А. Простякова, В.С. Немкова, В.Б. Демидовича и других [18, 44, 3, 90, 91, 84, 46, 10, 81, 42, 16, 26]. Модельные аналитические задачи с использованием типовых конечномерных аппроксимаций рассмотрены в [41, 46, 32]. Основы комбинированных моделей, когда для решения внешней электромагнитной задачи используется метод интегральных уравнений (метод вторичных источников), а для расчета электромагнитных и тепловых полей внутри нагреваемой заготовки – конечно-разностные и аналитические методы или их комбинации изложены в [34, 2, 17, 46, 79]. Опираясь на изложенные в вышеназванных трудах основы, можно построить адекватные математические модели для широкого круга реальных технологических ситуаций. Конкретные вопросы расчета электромагнитных и тепловых полей индукционных нагревательных установок рассмотрены в работах А.Е. Слухоцкого, Л.С. Зимина, М.Г. Когана, А.М. Павлова, Э.Я. Рапопорта, А.И. Данилушкина, А.Б. Кувалдина и других [90, 91, 29, 81, 85, 86, 23, 39, 40, 41]. Задача оптимизации технологии нагрева металла впервые была поставлена А.Г. Бутковским и развита в его фундаментальных монографиях [15]. В работах Э.Я. Рапопорта [85, 86, 100] предложен новый метод параметрической оптимизации процессов нестационарной теплопроводности при индукционном нагреве металла перед обработкой на деформирующем оборудовании. С позиций системного подхода рассмотрена общая задача совместной оптимизации процессов нагрева и последующего прессования по совокупному критерию качества. Показано, что наибольший эффект достигается не при решении задач оптимизации уже действующего оборудования, а при оптимизации оборудования на стадии проектирования и последующей оптимизации конструктивных и режимных параметров установки. В работе М.Ю. Лившица [36] исследуется задача совокупного оптимального проектирования и управления технологическими процессами тепломассопереноса. Для широкого класса индукционных нагревателей поставлены и решены задачи сосредоточенного и распределенного управления промышленными установками периодического и непрерывного действия в установившихся и нестационарных режимах работы. Общая идеология оптимального проектирования систем индукционного нагрева в комплексах «индукционная нагревательная установка – обработка металла давлением» дана в работах Л.С. Зимина. В работе [29] рассматривается проблема проектирования и функционирования систем индукционного нагрева (индукционный нагреватель – источник питания – система электроснабжения и управления) в едином комплексе с деформирующим оборудованием при достижении экстремальных технико-экономических показателей работы технологического комплекса в целом. В ряде работ, выполненных научной школой индукционного нагрева Самарского государственного технического университета [4, 14, 23, 29, 47, 80, 100], исследованы вопросы математического моделирования взаимосвязанных электромагнитных и тепловых полей изделий сложной формы и неоднородной физической структуры, разработаны на основе установленных закономерностей проблемно – ориентированные математические модели процесса периодического и непрерывного индукционного нагрева как объекта управления и даны рекомендации по конструированию индукционных систем для нагрева тел неканонического профиля. Моделированию индукционных нагревательных установок в комплексе обработки металлов давлением (нагревательные установки для сквозного нагрева под пластическую деформацию, поверхностной закалки) посвящены труды [10, 8, 2, 21, 44, 45, 89, 92. 90, 96]. Большой вклад в рассмотрение вопросов расчета, проектирования и практического применения индукционных установок для низкотемпературного нагрева ферромагнитных сталей на частоте 50 Гц в различных технологических процессах внес А.Б. Кувалдин [39]. В его трудах [39, 40, 41] приведены описания и характеристики установок индукционного нагрева ферромагнитных сталей, работающих в различных отраслях промышленности. В последние годы всё большее применение находят установки индукционного нагрева в таких нетрадиционных областях, как нефтеперерабатывающее производство, строительная индустрия, конверсионное производство и других отраслях промышленности [14, 29, 47, 4, 100, 23, 80]. Это обусловлено тенденцией к усовершенствованию уже существующих технологий, к максимальному использованию внутренних резервов самих процессов и установок, в рамках приоритетного энергосберегающего развития промышленности. В последние десятилетия одновременно с расширением области применения индукционного нагрева, происходит также модернизация установок самого индукционного нагрева и переход от классической технологии индукционного нагрева к новаторской. В качестве современных тенденций развития индукционного нагрева можно выделить индукционный нагрев алюминиевых заготовок, вращающихся в магнитном поле постоянного тока; разработка и исследование цилиндрических индукционных устройств с динамической дискретной подвижной частью; развитие индукционных систем для ремонтно-восстановительных технологий роторов газотурбинных двигателей; разработка и исследование устройств косвенного индукционного нагрева жидкостей в технологических комплексах различного назначения системы индукционного нагрева сопряженных физически неоднородных объектов (А.А. Базаров) и мн.др. [100, 23, 14, 4]. При разработке и исследовании сложных систем индукционного нагрева необходимо последовательное синергетическое решение нескольких важных задач – электромагнитной, тепловой, гидравлической, механической, задач оптимизации, и т.д. Для электрического расчёта индукционных устройств используют интегральные и численные методы. Интегральные методы основаны на введении вторичных источников поля, которые характеризуют реакцию тел, составляющих систему, на воздействие сторонних (первичных) источников. При этом сами тела заменяются вакуумом, что упрощает расчёт. Введение вторичных источников не является однозначным, что позволяет создавать различные расчётные модели, наиболее отвечающие конкретным целям [4]. Целью расчёта является определение вторичных источников, после чего легко найти любые параметры системы. Вторичные источники определяются решением интегральных уравнений, описывающих их взаимодействие друг с другом и с первичными источниками. Уравнения учитывают взаимодействия всех источников рассматриваемой системы, а не только соседних, поэтому интегральные методы наиболее удобны для расчёта квазистационарных систем. Это означает, что размеры устройства должны быть значительно меньше длины электромагнитной волны в воздухе. Все индукционные устройства подчиняются этому условию. Важным достоинством интегральных методов является то, что расчёт производиться только для областей, занятых вторичными источниками и составляющих обычно небольшую часть общего пространства, в котором существует поле. Однако использование интегральных методов зачастую связано с достаточно громоздким решением, обусловленным, например, сложной формой исследуемого объекта. Для рассматриваемого класса задач наиболее предпочтительными являются численные методы. Из численных методов наибольшее распространение получил метод конечных разностей (МКР) [24, 6]. Обладая такими достоинствами, как трехдиагональный характер матрицы жесткости, малый объем памяти в случае применения процедур для ленточных матриц, быстрое время счета, высокая устойчивость вычислительного процесса, метод конечных разностей все же не позволяет описать объект сложной формы. Метод граничных элементов (МГЭ) [6], сочетая достоинства аналитических и численных методов, позволяет легко описать объект любой формы, обладает высокой устойчивостью за счет малой ширины ленты матрицы жесткости, более точно описывает распределение температур при небольшом числе элементов по сравнению с МКР. Недостатком является условие неизменности свойств внутри элемента. В случае нелинейной задачи это приводит к существенной погрешности. Метод конечных элементов (МКЭ) [27, 28. 93] позволяет за счет большего числа элементов по сравнению с МГЭ решить и нелинейную задачу для тел сложной формы. Применение специальных процедур для ленточных матриц позволяет снизить объем памяти. Недостатком является лишь снижение устойчивости вычислительного процесса, что требует в некоторых случаях принятия необходимых мер, в частности уменьшения шага по времени. Практически неограниченные возможности МКЭ по описанию сложной геометрии исследуемых объектов и учету существующих нелинейностей при анализе полевых задач, универсальность формы построения вычислительных алгоритмов позволяет отдать ему предпочтение по сравнению с другими численными методами. Численные методы расчета устройств индукционного нагрева ферромагнитных заготовок стали применяться с начала 60-х годов XX века [40, 41]. Для математического моделирования устройств индукционного нагрева численные методы наиболее плодотворны и позволяют решать задачи, охватывающие расчет параметров и электромагнитного поля в ферромагнитной загрузке различной формы, расчет электрических и энергетических характеристик системы «индуктор – загрузка» и расчет температурного поля. Для рассматриваемого комплекса задач, решение которых необходимо для исследования и разработки трехфазного индуктора для нагрева цилиндрических ферромагнитных заготовок, выбор из существующих численных [24, 6 93, 27, 28] делается в пользу метода конечных элементов (МКЭ), поскольку он выгодно отличается от остальных следующими свойствами: 1) Физические свойства материалов, из которых состоит рассматриваемый объект, могут быть различными. 2) Криволинейная расчётная область может быть аппроксимирована с помощью прямолинейных конечных элементов и описана точно с помощью криволинейных конечных элементов. 3) Сетка из конечных элементов может не является регулярной ни геометрически, ни топологически. Это означает, что размеры и форма конечных элементов могут изменяться произвольно. 4) В МКЭ сравнительно легко учитываются смешанные граничные условия. 5) Существует база различных элементов позволяющих решать задачи как нестационарной теплопроводности, так и задачи теплообмена другой природы, кроме того, представляются широкие возможности моделирования задач. Особ енности индукционного нагрева ферромагнитной стали связаны в основном с нелинейной зависимостью относительной магнитной проницаемости от магнитной напряженности и наличием потерь на перемагничивание - явлением гистерезиса [40]. Фундаментальный вклад в теорию индукционного нагрева ферромагнетиков внес акад. Л.Р. Нейман [44]. В основе его подхода лежит замена известной петли гистерезиса зависимости Принципиально новый подход к решению задачи расчета параметров электромагнитного поля в ферромагнетике предложил Н.М. Родигин [88], который показал возможность численного расчета значений H и μ в слоях нагреваемого тела с использованием метода последовательных итераций. Таким методом может быть рассчитано усредненное значение μср для тел различной формы с дальнейшим использованием его в практических расчетах. Наиболее общее представление о процессах, происходящих при индукционном нагреве ферромагнитного проводящего тела, дает его заключительная стадия – горячий режим. Начало горячего режима соответствует образованию у поверхности слоя, нагретого выше точки магнитных превращений, в то время как остальная часть сечения, имеющая более низкую температуру, остается ферромагнитной. Здесь переменными величинами являются удельное сопротивление и магнитная проницаемость, причем последняя изменяется почти скачком на границе нагретого слоя. Металл становится как бы двухслойным. В предельном случае горячего режима все сечение прогрето насквозь и тогда удельное сопротивление и магнитную проницаемость можно считать постоянными. При рассмотрении горячего режима принимаются следующие допущения [90, 91]: а) имеются две резко разграниченные среды, на границе которых относительная магнитная проницаемость изменяется скачком от значения б) удельное сопротивление первой среды в её пределах неизменно; в) удельное сопротивление второй среды постоянно и равно удельному сопротивлению первой среды; г) магнитная проницаемость второй среды постоянна в её пределах и зависит от удельной мощности на поверхности первой среды. Как показывает экспериментальная проверка, расчеты, произведенные на основе указанных допущений, являются достаточно точными для решения технических задач [91, 26, 88]. Перечисленные допущения можно обосновать следующим образом [46, 40]: а) магнитная проницаемость в области температур, близких к точке магнитных превращений, изменяется очень резко, и для приближенного рассмотрения это изменение может быть заменено скачком. б) кривая зависимости удельного сопротивления всех сортов стали от температуры выше точки магнитных превращений становится пологой. Перепад температуры по толщине первой среды обычно не превышает 150-200°С, что дает основание принять для первой среды значение удельного сопротивления, соответствующее 800-850°С; в) удельное сопротивление на границе сред изменяется непрерывно, постепенно уменьшаясь с ростом глубины. Магнитная проницаемость имеет на границе значение, зависящее от степени магнитного насыщения стали, и увеличивается с глубиной. Приведенные в [90] распределения плотности тока по сечению показывают, что наличие второй среды с Применение магнитопроводов, изготовленных из листов электротехнической стали, позволяет изменить распределение индуктированного тока на поверхности заготовки. При использовании магнитопровода концентрация тока под индуктором резко повышается. По ширине паза в магнитопроводе поверхностная плотность тока изменяется сравнительно мало и быстро падает за его пределами, с внешней стороны это проявляется в резко очерченной форме нагретой полосы. Возможность влияния на распределение индуктируемого тока используется в ряде случаев для выравнивания нагрева при индукционном нагреве деталей сложной формы. Коэффициент полезного действия индукторов с магнитопроводами обычно не ниже 75-80% [90]. Ток в индуктирующем проводе оттесняется к открытой стороне паза магнитопровода независимо от кольцевого эффекта и эффекта близости. Благодаря высокой магнитной проницаемости магнитопровода магнитное поле с обратной стороны провода пренебрежительно мало по сравнению с магнитным полем на его наружной поверхности: в пределе при
|

 эквивалентным по площади эллипсом. Потери на перемагничивание оказываются пренебрежительно малы по сравнению с потерями за счет индуцированных в стали токов уже при значениях магнитной напряженности на поверхности стали 5 кА/м [91] и обычно в расчетах устройств индукционного нагрева ферромагнитной стали не учитываются, так как в них используются ещё более сильные электромагнитные поля. Исследования Л.Р. Неймана были продолжены и развиты другими авторами, в первую очередь А.В. Донским [26] и А.Е. Слухоцким [91].
эквивалентным по площади эллипсом. Потери на перемагничивание оказываются пренебрежительно малы по сравнению с потерями за счет индуцированных в стали токов уже при значениях магнитной напряженности на поверхности стали 5 кА/м [91] и обычно в расчетах устройств индукционного нагрева ферромагнитной стали не учитываются, так как в них используются ещё более сильные электромагнитные поля. Исследования Л.Р. Неймана были продолжены и развиты другими авторами, в первую очередь А.В. Донским [26] и А.Е. Слухоцким [91]. в пределах первой среды до
в пределах первой среды до  на границе второй;
на границе второй; оказывает значительное влияние на распределение плотности тока в нагреваемом слое. Чем больше магнитная проницаемость второй среды, тем равномернее это распределение, а, следовательно, и распределение плотности мощности по сечению нагреваемого слоя. С уменьшением глубины прогрева кривая зависимости плотности тока от глубины становится все более пологой и равномерность нагрева повышается. При глубинах прогрева, превышающих горячую глубину проникновения тока, влияние второй среды ослабляется, и зависимость плотности тока от глубины приближается к экспоненте. При этом основная часть тепловой энергии выделяется в слое глубины проникновения тока, остальная же часть металла прогревается за счет теплопроводности.
оказывает значительное влияние на распределение плотности тока в нагреваемом слое. Чем больше магнитная проницаемость второй среды, тем равномернее это распределение, а, следовательно, и распределение плотности мощности по сечению нагреваемого слоя. С уменьшением глубины прогрева кривая зависимости плотности тока от глубины становится все более пологой и равномерность нагрева повышается. При глубинах прогрева, превышающих горячую глубину проникновения тока, влияние второй среды ослабляется, и зависимость плотности тока от глубины приближается к экспоненте. При этом основная часть тепловой энергии выделяется в слое глубины проникновения тока, остальная же часть металла прогревается за счет теплопроводности.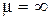 поле в магнитопроводе равно нулю. Поэтому при любой форме провода в такой системе наблюдается односторонний поверхностный эффект.
поле в магнитопроводе равно нулю. Поэтому при любой форме провода в такой системе наблюдается односторонний поверхностный эффект.


