Постановка задачи моделирования
Настоящий раздел посвящен разработке математической модели и исследованию электромагнитных и тепловых процессов в системе «трехфазный индуктор поперечного магнитного поля – цилиндрическая заготовка» с целью определения взаимосвязи электромагнитных и тепловых полей и качественной оценки характера распределения внутренних источников тепла и температурного поля в заготовке и элементах конструкции индуктора. Индукционный нагрев является одним из наиболее сложных электротермических процессов и в строгой постановке требует рассмотрения взаимосвязанных явлений разной физической природы. Полное моделирование процесса индукционного нагрева требует совместного решения электромагнитной задачи для всей системы, внутренней электротепловой задачи и задачи внешнего теплообмена. Для решения этих задач необходимо знание характера электромагнитных и тепловых процессов и средств их количественного описания (моделирования). Характер распределения вихревых токов в цилиндрической заготовке зависит от многих факторов, обусловленных геометрическими размерами системы, электро- и теплофизическими свойствами материала, частотой источника питания, температурой нагрева и др. Нагрев немагнитных материалов сопровождается существенным изменением удельного сопротивления в процессе нагрева, а индукционный нагрев ферромагнитных материалов, кроме того, характеризуется существенным изменением магнитной проницаемости металла и, соответственно, глубины проникновения тока. К тому же, как известно из многочисленных источников [46, 18, 21, 81, 40, 45], даже для тел правильной цилиндрической формы, у которых продольные и поперечные размеры соизмеримы, характерно наличие существенных краевых эффектов в распределении напряженности магнитного поля, которые в конечном итоге оказывают влияние на характер распределения внутренних источников тепла. Наличие ферромагнитных масс сложной конфигурации еще более усложняет моделирование электромагнитных и тепловых полей в исследуемой системе. При исследовании любой сложной системы принимается ряд общих и специфических допущений, корректность которых зависит от конкретной системы. К общим допущениям при решении электромагнитной задачи можно отнести: отсутствие запаздывания электромагнитной волны в воздухе; расчет установившихся электромагнитных процессов для величин, меняющихся по гармоническому закону; однозначность зависимости магнитной проницаемости от напряженности магнитного поля; магнитная проницаемость считается действительной величиной (т.к. потери на гистерезис при нагреве ферромагнитного тела много меньше потерь на вихревые токи). Для успешного решения указанных задач требуется разработка численных методов, качественная реализация их в виде программных средств, обеспечение диалогового общения пользователя с ЭВМ, так как аналитические методы имеют жесткие ограничения по области применения и используются обычно для геометрически простых систем или частей сложной системы, как правило, в линейной постановке. Такая технология исследований с широким применением цифровых моделей и ЭВМ получила название вычислительного эксперимента [78]. Вычислительный эксперимент отличается от физического объемом и качеством информации. В вычислительном эксперименте объем получаемой информации не ограничивается числом датчиков и их быстродействием. Оказываются возможными вычислительные эксперименты в очень широком диапазоне конструктивных параметров и режимов работы устройств, включая аварийные. Изменение физических свойств материалов, геометрических размеров позволяет просмотреть всю возможную номенклатуру. Важной особенностью вычислительного эксперимента является повторяемость результатов, отсутствие случайной ошибки, связанной с действием неучтенных факторов. Для составления целостной картины изменения плотности тока и мощности в загрузке в процессе нагрева и возможности аналитического описания функции распределения внутренних источников тепла требуется последовательное решение электромагнитной и тепловой задач. Разделение во времени процедур расчета электромагнитного поля и теплового поля объясняется разной инерционностью этих процессов. Электромагнитная задача формулируется как квазистационарная, а тепловая имеет в дифференциальном уравнении временную производную первого порядка. Все это позволяет создать полностью или частично независимые процедуры расчетов электромагнитных и тепловых полей. Модели, учитывающие взаимное влияние электромагнитного и температурного полей в процессе нагрева, так называемые электротепловые модели, дают исчерпывающую характеристику индукционного устройства с точки зрения потребления энергии от внешнего источника питания и выделения ее в загрузке. Предлагаемая конструкция индукционной системы отличается наличием свойств, характерных для электрических машин, в частности, асинхронных. Это предполагает использование сходных методов расчета, хотя и имеющих различные цели. Если для асинхронной машины требуется минимизировать потери мощности на тепло и обеспечить максимальный вращающий момент, то для индуктора главным является получение максимальной мощности внутренних источников тепла в загрузке. Тем не менее, наличие магнитопровода с чередующимися по фазе токовыми катушками приводит к необходимости оптимизировать распределение индукции в зубцах и уменьшить поля рассеяния в зазоре [22, 13, 19, 25. 35]. Это объединяет две задачи – проектирования индуктора и двигателя. В общем случае возможно формирование как неподвижного поля относительно загрузки, так и вращающегося, что позволяет решать дополнительные технологические задачи [73, 76, 77, 59, 50, 55, 56, 60, 61, 62, 63, 72, 48? 68]. В предлагаемой работе будет рассмотрен только режим неподвижного магнитного поля, что исключает создание вращающего момента и необходимость фиксации загрузки. Геометрическая модель исследуемой индукционной системы представлена на рис. 2.1.
Рисунок 2.1 — Геометрическая модель исследуемой установки: 1 - магнитопровод индуктора; 2 - воздушный зазор; 3 - футеровка; 4 - изоляция; 5 - нагреваемое изделие; 6 - обмотка
Так как индуктор нагревательной установки выполнен в виде статора асинхронной машины, её с некоторым допущением можно рассматривать как асинхронный двигатель с массивным ротором, работающий в режиме короткого замыкания. Известно, что любая электрическая машина является системой взаимно перемещающихся контуров тока с распределенными параметрами [51]. Наиболее распространенный способ математического моделирования процессов в такой системе – это представление её в виде электрической цепи с сосредоточенными параметрами – схемы замещения [19, 35]. Однако в исследуемом объекте при таком аналитическом расчете некоторые параметры магнитной цепи и схемы замещения не могут претендовать на точность уже по причине большого воздушного зазора между заготовкой и индуктором, так как это не характерно для асинхронных машин. Кроме того, схемы замещения удобно использовать при расчете интегральных параметров, например, момента, но никак не для определения распределенных источников тепла. Это в очередной раз подчеркивает неприемлемость аналитического расчета для электромагнитной задачи. Особенностью рассматриваемой индукционной системы является сильная зависимость параметров от магнитного состояния загрузки. Поэтому повышение точности расчета магнитной проницаемости в течение всего процесса нагрева является первоочередной задачей. Существующие программные комплексы чаще всего обеспечивают зависимости магнитной проницаемости от напряженности магнитного поля. Введение температурной зависимости обеспечивается внешним воздействием на вводимые параметры, что требует объединения электромагнитной и тепловой задач. Еще одна проблема состоит в том, что нелинейные электромагнитные задачи с учетом кривых намагничивания решаются для нестационарных процессов. Чаще всего на первом этапе решается нелинейная магнитная задача, где определяются основные магнитные параметры, а затем уже решается линейная (с постоянной магнитной проницаемостью в различных зонах объекта) стационарная (гармонический анализ) электромагнитная задача. Для индуктора с магнитной системой такой подход не обеспечивает достаточной точности расчетов, поэтому предлагается более сложный алгоритм, содержащий решение нелинейной стационарной задачи совместно с решением тепловой задачи и пересчетом распределения магнитной проницаемости на каждом шаге. В общем случае процесс индукционного нагрева цилиндрической заготовки в индукторе с замкнутым магнитопроводом описывается нелинейной взаимосвязанной системой уравнений Максвелла и Фурье соответственно для электромагнитного и теплового полей с соответствующими краевыми условиями [46, 43]:
Здесь
T - температура; t - время;
Система уравнений (2.1) - (2.4) дополняется граничными условиями для электромагнитной задачи: используются условия равенства функции нулю на бесконечно удаленной границе Для тепловой задачи используется более широкий спектр граничных условий – от условия симметрии (граничные условия второго рода) до теплообмена между соприкасающимися телами (граничное условие четвертого рода).
|


 (2.1)
(2.1)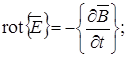 (2.2)
(2.2)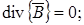 (2.3)
(2.3) (2.4)
(2.4)
 . (2.5)
. (2.5)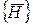 ,
, 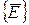 ,
,  - векторы напряженности магнитного и электрического полей и магнитной индукции;
- векторы напряженности магнитного и электрического полей и магнитной индукции;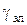 - удельная электропроводимость;
- удельная электропроводимость;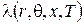 - компоненты тензора теплопроводности (теплопроводность как функция температуры представляется кубическим сплайном);
- компоненты тензора теплопроводности (теплопроводность как функция температуры представляется кубическим сплайном);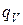 - удельная мощность тепловыделения (в линейной постановке - константа, в нелинейной постановке - задаваемая кубическим сплайном в функции температуры);
- удельная мощность тепловыделения (в линейной постановке - константа, в нелинейной постановке - задаваемая кубическим сплайном в функции температуры);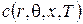 - удельная теплоемкость (в нелинейном случае это функция температуры, аппроксимированная кубическими сплайнами);
- удельная теплоемкость (в нелинейном случае это функция температуры, аппроксимированная кубическими сплайнами); - плотность,
- плотность,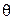 - угловая координата.
- угловая координата.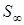 и условие симметрии на поверхности симметрии
и условие симметрии на поверхности симметрии 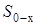 , которое заключается в равенстве нулю производной от функции.
, которое заключается в равенстве нулю производной от функции.


