Рассмотрим в пространстве прямоугольную систему координат Oxyz. Выделим на координатных осях Ox, Oy и Oz единичные векторы (орты), обозначаемые 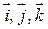 соответственно.
соответственно.
Выберем произвольный вектор  пространства и совместим его начало с началом координат:
пространства и совместим его начало с началом координат: 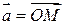 .
.
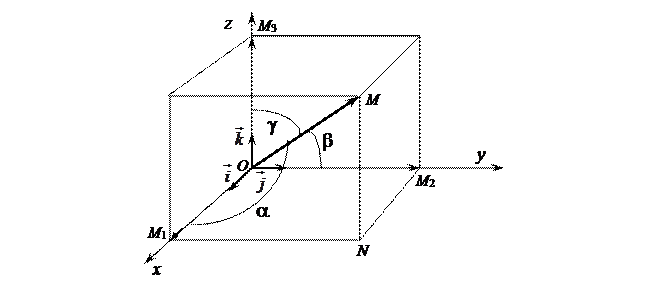
Найдем проекции вектора  на координатные оси. Проведем через конец вектора
на координатные оси. Проведем через конец вектора 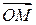 плоскости, параллельные координатным плоскостям. Точки пересечения этих плоскостей с осями обозначим соответственно через
плоскости, параллельные координатным плоскостям. Точки пересечения этих плоскостей с осями обозначим соответственно через 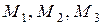 . Получим прямо-угольный параллелепипед, одной из диагоналей которого является вектор
. Получим прямо-угольный параллелепипед, одной из диагоналей которого является вектор 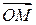 . Тогда
. Тогда  ,
, 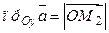 ,
, 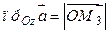 . По определению суммы нескольких векторов находим
. По определению суммы нескольких векторов находим 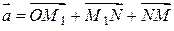 . А так как
. А так как 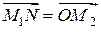 ,
, 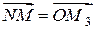 , то
, то
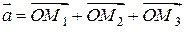
Но 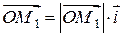 ,
, 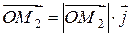 ,
, 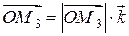 .
.
Обозначим проекции вектора 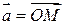 на оси Ox, Oy и Oz соответственно через
на оси Ox, Oy и Oz соответственно через 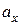 ,
, 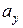 и
и 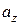 , т.е.
, т.е. 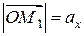 ,
, 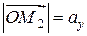 и
и 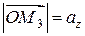 .
.
Тогда получаем
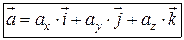 . (1.2)
. (1.2)
Формула (1.2) является основной в векторном исчислении и называется разложением вектора по ортам координатных осей. Числа 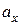 ,
, 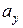 и
и 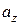 называются координатами вектора
называются координатами вектора  , т.е. координаты вектора есть его проекции на соответствующие координатные оси. Векторное равенство (1.2) часто записывается в символическом виде:
, т.е. координаты вектора есть его проекции на соответствующие координатные оси. Векторное равенство (1.2) часто записывается в символическом виде: 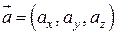 .
.
Зная проекции вектора  , можно легко найти выражение для модуля вектора. На основании теоремы о длине диагонали прямоугольного параллелепипеда можно записать
, можно легко найти выражение для модуля вектора. На основании теоремы о длине диагонали прямоугольного параллелепипеда можно записать  , т.е.
, т.е.
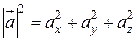 .
.
Отсюда
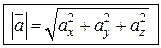 , (1.3)
, (1.3)
т.е. модуль вектора равен квадратному корню из суммы квадратов его проекций на оси координат.
Пусть углы вектора  с осями Ox, Oy и Oz соответственно равны a, b и g. По свойству проекции вектора на ось имеем
с осями Ox, Oy и Oz соответственно равны a, b и g. По свойству проекции вектора на ось имеем
 ,
,  ,
, 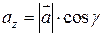 .
.
Или,
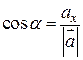 ,
, 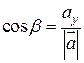 ,
, 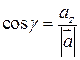 . (1.4)
. (1.4)
Числа 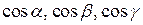 называются направляющими косинусами вектора
называются направляющими косинусами вектора  .
.
Подставляя полученные косинусы в выражение квадрата модуля вектора  , получаем
, получаем
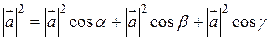 .
.
Сократив на 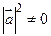 , получаем соотношение
, получаем соотношение
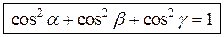 , (1.5)
, (1.5)
т.е. сумма квадратов направляющих косинусов ненулевого вектора равна единице.
Легко заметить, что координаты единичного вектора 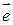 являются числа
являются числа 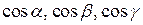 , т.е.
, т.е. 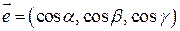 .
.
Итак, задав координаты вектора, всегда можно определить его модуль и направление, т.е. сам вектор.

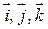 соответственно.
соответственно. пространства и совместим его начало с началом координат:
пространства и совместим его начало с началом координат: 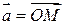 .
.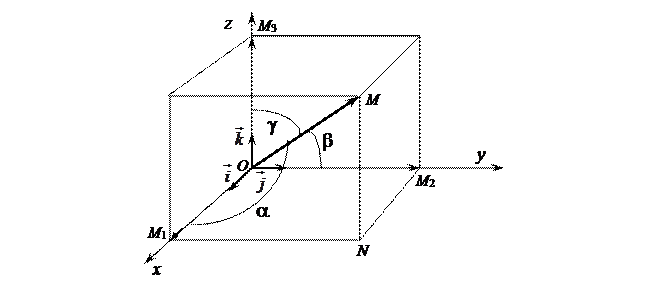
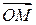 плоскости, параллельные координатным плоскостям. Точки пересечения этих плоскостей с осями обозначим соответственно через
плоскости, параллельные координатным плоскостям. Точки пересечения этих плоскостей с осями обозначим соответственно через 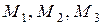 . Получим прямо-угольный параллелепипед, одной из диагоналей которого является вектор
. Получим прямо-угольный параллелепипед, одной из диагоналей которого является вектор  ,
, 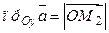 ,
, 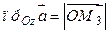 . По определению суммы нескольких векторов находим
. По определению суммы нескольких векторов находим 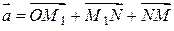 . А так как
. А так как 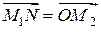 ,
, 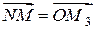 , то
, то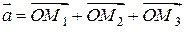
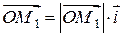 ,
, 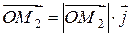 ,
, 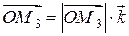 .
.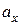 ,
, 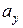 и
и 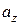 , т.е.
, т.е. 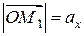 ,
, 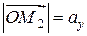 и
и 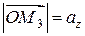 .
.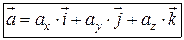 . (1.2)
. (1.2)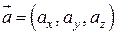 .
. , т.е.
, т.е.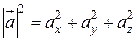 .
.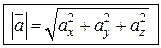 , (1.3)
, (1.3) ,
,  ,
, 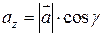 .
.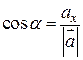 ,
, 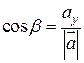 ,
, 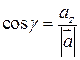 . (1.4)
. (1.4)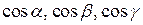 называются направляющими косинусами вектора
называются направляющими косинусами вектора 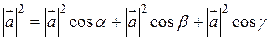 .
.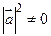 , получаем соотношение
, получаем соотношение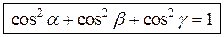 , (1.5)
, (1.5)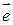 являются числа
являются числа 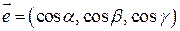 .
.


