Системы векторов
Для характеристики взаимного расположения векторов в пространстве вводится понятие линейной зависимости между векторами. Вектор
Числа
Определение 2.1. Система векторов
Определение 2.2. Если равенство (2.2) возможно лишь в случае, когда
Рассмотрим ряд теорем, которые примем без доказательства. Теорема 2.1. Два вектора Теорема 2.2. Если
Теорема 2.3. Три вектора Теорема 2.4. Если векторы
Теорема 2.5. Всякие четыре вектора трехмерного пространства линейно зависимы.
Назовем векторы
…………………..
единичными векторами n -мерного пространства. Отметим, что система единичных векторов n -мерного пространства линейно независима. Теорема 2.6. Любой вектор n -мерного пространства является линейной комбинацией единичных векторов этого пространства, т.е.
Таким образом, всякий вектор n -мерного пространства равен сумме произведений его координат на соответствующие единичные векторы.
Пример 2.1. Выяснить, будет ли данная система векторов линейно зависимой или независимой
Решение. Составим их линейную комбинацию:
или
Такое векторное уравнение эквивалентно следующей системе уравнений:
Найдем ранг системы. Составляем матрицу системы и приводим к ступенчатому виду:
Так как Например, частным решением является: ,
|

 называется линейной комбинациейвекторов системы
называется линейной комбинациейвекторов системы  , если существуют такие числа
, если существуют такие числа  , что
, что . (2.1)
. (2.1) называются коэффициентами линейной комбинации. В этом случае говорят, что вектор
называются коэффициентами линейной комбинации. В этом случае говорят, что вектор  или вектор
или вектор  . Введением понятия линейной комбинации мы объединили понятия сложения векторов и умножения вектора на число.
. Введением понятия линейной комбинации мы объединили понятия сложения векторов и умножения вектора на число. . (2.2)
. (2.2) , то система
, то система  называется линейно независимой.
называется линейно независимой. и
и  линейно зависимы тогда и только тогда, когда они коллинеарны.
линейно зависимы тогда и только тогда, когда они коллинеарны. той же плоскости можно единственным образом разложить по ним, т.е. представить в виде
той же плоскости можно единственным образом разложить по ним, т.е. представить в виде . (2.3)
. (2.3) линейно зависимы тогда и только тогда, когда они компланарны.
линейно зависимы тогда и только тогда, когда они компланарны. . (2.4)
. (2.4) ,
, ,
, ,
,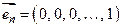
 .
. .
.
 .
. .
. ~
~  ~
~  .
. , то система имеет бесчисленное множество решений, среди которых есть ненулевой. Значит, система векторов линейно зависима.
, то система имеет бесчисленное множество решений, среди которых есть ненулевой. Значит, система векторов линейно зависима. . Значит,
. Значит,  , т.е указанная система векторов линейно зависима.
, т.е указанная система векторов линейно зависима.


