Линейные операции над векторами
В математике и ее приложениях различают два типа величин: скалярные и векторные. Скалярной величиной или скаляром называется величина, которая полностью определяется своим численным значением. Примерами скалярных величин являются: площадь, длина, объем, температура, масса, работа и т.д. Другие величины, такие как скорость, ускорение, сила, определяются не только своим численным значением, но и направлением. Такие величины называют векторными.
Геометрическим вектором называется направленный отрезок AB с начальной точкой A и конечной точкой B.
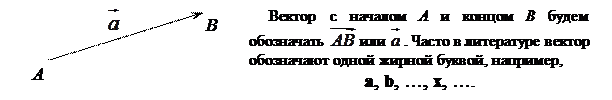
Вектор 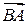 называется противоположным вектору
называется противоположным вектору  . Вектор, противоположный вектору
. Вектор, противоположный вектору  обозначается
обозначается  .
.
Модулем или длиной вектора  называется длина отрезка и обозначается
называется длина отрезка и обозначается 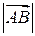 .
.
Вектор, длина которого равна нулю, называется нулевым вектором и обозначается 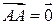 . Нулевой вектор направления не имеет.
. Нулевой вектор направления не имеет.
Вектор, длина которого равна единице, называется единичным вектором и обозначается 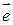 . Единичный вектор, направление которого совпадает с направлением вектора
. Единичный вектор, направление которого совпадает с направлением вектора  , называется ортом вектора
, называется ортом вектора  и обозначается
и обозначается 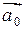 .
.


Два вектора  и
и  называются равными, если: а) они коллинеарны; б) одинаково направлены; в) длины их равны. Например,
называются равными, если: а) они коллинеарны; б) одинаково направлены; в) длины их равны. Например,  Равные векторы называют также свободными. Свободные векторы можно перемещать параллельно самим себе.
Равные векторы называют также свободными. Свободные векторы можно перемещать параллельно самим себе.
Для свободных векторов определены линейные операции сложения, вычитания и умножение вектора на действительное число.
Суммойдвух векторов  и
и  называется вектор
называется вектор 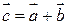 , начало которого совпадает с началом вектора
, начало которого совпадает с началом вектора  , а конец – с концом вектора
, а конец – с концом вектора  , при условии, что вектор
, при условии, что вектор  отложен из конца вектора
отложен из конца вектора  .
.
Вектор 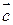 получается по правилу треугольника или по правилу параллелограмма.
получается по правилу треугольника или по правилу параллелограмма.
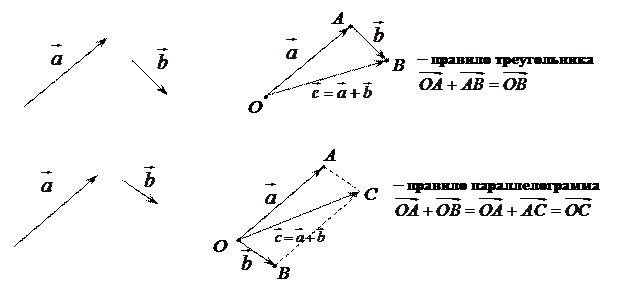
Аналогично определяется сумма трех и более векторов. Суммой n векторов 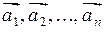 называется вектор, начало которого совпадает с началом первого вектора
называется вектор, начало которого совпадает с началом первого вектора  , конец – с концом последнего
, конец – с концом последнего 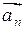 при условии, что каждый последующий вектор
при условии, что каждый последующий вектор 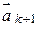 отложен из конца предыдущего
отложен из конца предыдущего 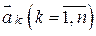 . Указанный способ построения суммы конечного числа n векторов называется правилом замыкающей. Например, на рисунке изображена сумма трех векторов
. Указанный способ построения суммы конечного числа n векторов называется правилом замыкающей. Например, на рисунке изображена сумма трех векторов
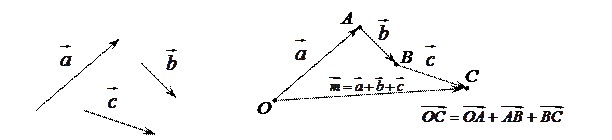
Разностьюдвух векторов  и
и  называется вектор
называется вектор 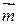 , который в сумме с вектором
, который в сумме с вектором  дает вектор
дает вектор  , т.е.
, т.е.
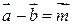 , если
, если 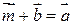 .
.
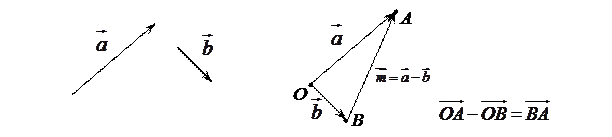
Можно вычитать векторы по правилу:  , т.е. вычитание векторов заменить сложением вектора
, т.е. вычитание векторов заменить сложением вектора  с вектором, противоположным вектору
с вектором, противоположным вектору  .
.
Отметим, что в параллелограмме, построенном на векторах  и
и  , одна диагональ является суммой векторов
, одна диагональ является суммой векторов  и
и  , а другая – разностью.
, а другая – разностью.
Произведением вектора  на действительное число (скаляр) l называется вектор
на действительное число (скаляр) l называется вектор
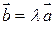 ,
,
удовлетворяющий условиям: 1) 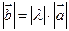 ; 2)
; 2)  и
и  одинаково направлены при l>0; 3)
одинаково направлены при l>0; 3)  и
и  имеют противоположные направления при l<0.
имеют противоположные направления при l<0.
Например, если дан вектор  , то векторы
, то векторы  и
и  имеют вид
имеют вид

Очевидно,  , если l=0 или
, если l=0 или  .
.
Из определения произведения вектора на число следуют свойства этого произведения:
1) если 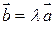 , то
, то  . Наоборот, если
. Наоборот, если 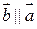 , (
, ( ), то при некотором l верно равенство
), то при некотором l верно равенство 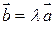 ;
;
2) всегда 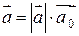 , т.е. каждый вектор равен произведению его модуля на орт.
, т.е. каждый вектор равен произведению его модуля на орт.
Линейные операции над векторами обладают следующими свойствами:
1. 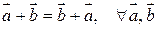 , т.е. сложение векторов коммутативно;
, т.е. сложение векторов коммутативно;
2. 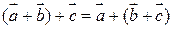 , т.е. сложение векторов ассоциативно;
, т.е. сложение векторов ассоциативно;
3.  ;
;
4. 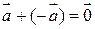 ;
;
5.  , т.е. умножение вектора на число ассоциативно;
, т.е. умножение вектора на число ассоциативно;
6. 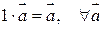 ;
;
7. 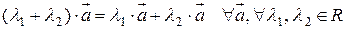 , т.е. умножение вектора на число дистрибутивно по отношению к сложению чисел;
, т.е. умножение вектора на число дистрибутивно по отношению к сложению чисел;
8. 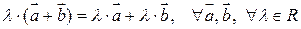 , т.е. умножение вектора на число дистрибутивно по отношению к сложению векторов.
, т.е. умножение вектора на число дистрибутивно по отношению к сложению векторов.
Множество всех векторов пространства (плоскости) с введенными выше операциями сложения векторов и умножения векторов на число, удовлетворяющими аксиомам 1. – 8., называется линейным или векторным пространством и обозначается 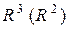 .
.

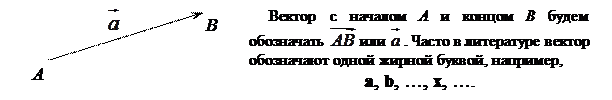
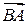 называется противоположным вектору
называется противоположным вектору  . Вектор, противоположный вектору
. Вектор, противоположный вектору  обозначается
обозначается  .
.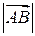 .
.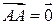 . Нулевой вектор направления не имеет.
. Нулевой вектор направления не имеет.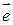 . Единичный вектор, направление которого совпадает с направлением вектора
. Единичный вектор, направление которого совпадает с направлением вектора 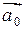 .
.

 называются равными, если: а) они коллинеарны; б) одинаково направлены; в) длины их равны. Например,
называются равными, если: а) они коллинеарны; б) одинаково направлены; в) длины их равны. Например,  Равные векторы называют также свободными. Свободные векторы можно перемещать параллельно самим себе.
Равные векторы называют также свободными. Свободные векторы можно перемещать параллельно самим себе.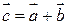 , начало которого совпадает с началом вектора
, начало которого совпадает с началом вектора 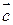 получается по правилу треугольника или по правилу параллелограмма.
получается по правилу треугольника или по правилу параллелограмма.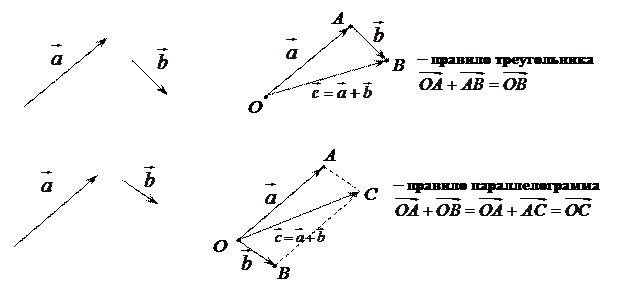
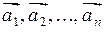 называется вектор, начало которого совпадает с началом первого вектора
называется вектор, начало которого совпадает с началом первого вектора  , конец – с концом последнего
, конец – с концом последнего 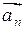 при условии, что каждый последующий вектор
при условии, что каждый последующий вектор 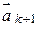 отложен из конца предыдущего
отложен из конца предыдущего 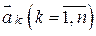 . Указанный способ построения суммы конечного числа n векторов называется правилом замыкающей. Например, на рисунке изображена сумма трех векторов
. Указанный способ построения суммы конечного числа n векторов называется правилом замыкающей. Например, на рисунке изображена сумма трех векторов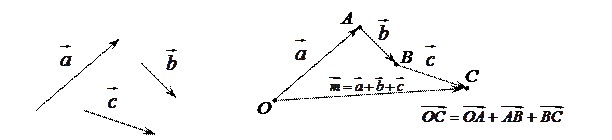
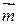 , который в сумме с вектором
, который в сумме с вектором 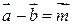 , если
, если 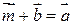 .
.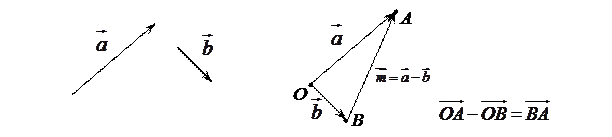
 , т.е. вычитание векторов заменить сложением вектора
, т.е. вычитание векторов заменить сложением вектора 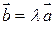 ,
,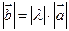 ; 2)
; 2)  и
и  имеют вид
имеют вид
 , если l=0 или
, если l=0 или  .
. . Наоборот, если
. Наоборот, если 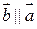 , (
, ( ), то при некотором l верно равенство
), то при некотором l верно равенство 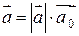 , т.е. каждый вектор равен произведению его модуля на орт.
, т.е. каждый вектор равен произведению его модуля на орт.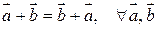 , т.е. сложение векторов коммутативно;
, т.е. сложение векторов коммутативно;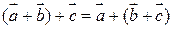 , т.е. сложение векторов ассоциативно;
, т.е. сложение векторов ассоциативно; ;
;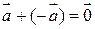 ;
; , т.е. умножение вектора на число ассоциативно;
, т.е. умножение вектора на число ассоциативно;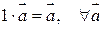 ;
;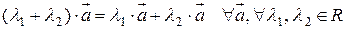 , т.е. умножение вектора на число дистрибутивно по отношению к сложению чисел;
, т.е. умножение вектора на число дистрибутивно по отношению к сложению чисел;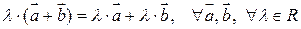 , т.е. умножение вектора на число дистрибутивно по отношению к сложению векторов.
, т.е. умножение вектора на число дистрибутивно по отношению к сложению векторов.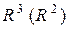 .
.


