Разложение вектора по базису
Определение 2.3. Базисом данной системы векторов называют такую подсистему, векторы которой линейно независимы, а любой другой вектор системы является их линейной комбинацией. В частности, базисом на прямой называется любой ненулевой вектор Определение 2.4. Рангом системы векторов называется максимальное число линейно независимых векторов этой системы, т.е. число векторов в базисе. Для вычисления ранга системы векторов нужно по столбцам составить матрицу из координат этих векторов и вычислить ее ранг, который будет равен рангу этой системы векторов. Пример 2.2. Найти ранг системы, состоящей из трех векторов:
Решение. Составим матрицу из координат этих векторов:
Так как
Так системы , Сформулируем следующее следствие, которое примем без доказательства. Следствие. Система, состоящая более чем из n n -мерных векторов, линейна зависима. Выше понятия базиса и ранга системы векторов были применены для систем, состоящих из конечного числа векторов. Но сформулированное следствие позволяет распространить их на системы с бесконечным числом векторов. Теперь мы можем быть уверены, что базис любой такой системы состоит из конечного числа векторов, не превосходящего n (размерности пространства). В частности, можно говорить о базисе и ранге системы всех n -мерных векторов, т.е. всего n -мерного пространства. Одним из базисов этого пространства является система единичных векторов Важное значение имеет следующая теорема, которую примем без доказательства. Теорема 2.7. Любой вектор
Числа Большое значение этой теоремы состоит в том, что на ее основе изучение бесчисленного многообразия векторов n -мерного пространства можно свести к изучению конечного множества векторов базиса.
Пример 2.3. Показать, что векторы Решение. 1) Убедимся, что векторы
Таким образом, получаем следующую систему уравнений
Итак, векторы
[ Чтобы убедиться, что векторы
Мы тем самым показываем, что векторы
2) Пусть
Следовательно,
Таким образом, получаем следующую систему уравнений
Итак, ,
|

 на этой прямой. Базисом на плоскости называются любые два независимых (неколлинеарных) вектора
на этой прямой. Базисом на плоскости называются любые два независимых (неколлинеарных) вектора  и
и  этой плоскости, взятых в определенном порядке. Базисом в трехмерном пространстве называются любые три линейно независимых (некомпланарных) вектора
этой плоскости, взятых в определенном порядке. Базисом в трехмерном пространстве называются любые три линейно независимых (некомпланарных) вектора  . Векторы, составляющие базис, называются базисными. Базис принято обозначать следующим образом:
. Векторы, составляющие базис, называются базисными. Базис принято обозначать следующим образом:  .
. .
. ~
~ 
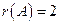 , следовательно, три вектора линейно зависимы и базис не образуют.
, следовательно, три вектора линейно зависимы и базис не образуют. ,
,  и
и  .
. .
. . (2.5)
. (2.5) в разложении (2.5) называются координатами вектора
в разложении (2.5) называются координатами вектора 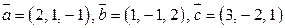 образуют базис. Найти координаты вектора
образуют базис. Найти координаты вектора  в этом базисе.
в этом базисе. и
и  линейно независимы, т.е. векторное равенство
линейно независимы, т.е. векторное равенство  возможно лишь при
возможно лишь при  . Действительно,
. Действительно, .
. Û
Û  .
. .
. - координаты вектора
- координаты вектора  в этом базисе, т.е.
в этом базисе, т.е. .
. .
. Û
Û  .
.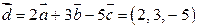 .
.


