Проекция вектора на ось
Назовем осью L прямую, на которой задано направление. Углом между двумя векторами (или между вектором и осью, или между двумя осями) называется наименьший угол j, на который нужно повернуть один вектор (ось), чтобы он совпал по направлению с другим вектором (осью).
Перпендикулярность векторов Проекцией вектора
Рассмотрим некоторые основные свойства проекций. Свойство 1. Проекция вектора
Следствие 9.1. Проекция вектора на ось положительная (отрицательная), если вектор образует с осью острый (тупой) угол, и равна нулю, если этот угол – прямой. Следствие 9.2. Проекции равных векторов на одну и ту же ось равны между собой.
Свойство 2. Проекция суммы нескольких векторов на одну и ту же ось равна сумме их проекций на эту ось, т.е.
Свойство 3. При умножении вектора
Таким образом, линейные операции над векторами приводят к соответствующим линейным операциям над проекциями этих векторов.
|
и 
обозначим 
.
на ось L называется длина отрезка 
, заключенного между ортогональными проекциями начала и конца вектора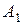 
до 
совпадает с направлением оси, и со знаком «-», если не совпадает.
. (1.1)
.
.
