Интерпретация результатов. После того как найдена единичная матрица, следует интерпретировать получен­ные результаты

После того как найдена единичная матрица, следует интерпретировать получен­ные результаты. В данном случае при наличии входных данных об ожидаемых прибылях и дисперсии прибылей по всем рассматриваемым компонентам, при наличии коэффициентов линейной корреляции каждой пары компонентов и ожидаемой отдаче 14% наше решение является оптимальным. Слово «оптималь­ный» означает, что полученное решение дает самую низкую дисперсию при ожи­даемой прибыли 14%. Мы можем определить это значение дисперсии, но сначала интерпретируем результаты.

Первые четыре значения, от X₁ до Х₄ дают нам веса, т.е. доли инвестируемых средств, для получения оптимального портфеля с 14%-ой ожидаемой прибылью. Нам следует инвестировать 12,391% в Toxico, 12,787% в Incubeast, 38,407% в LA Garb и 36,424% в сберегательный счет. Если мы хотим инвестировать 50 000 дол­ларов, то получим:

 

Акция	Процент	(* 50000 =) сумма инвестиций
Toxico	0,12391	$6195,50
Incubeast	0,12787	$6393,50
LA Garb	0,38407	$19 203,50
Сберегательный счет	0,36424	$18212,00

 

Таким образом, в Incubeast мы бы инвестировали 6393,50 доллара. Теперь допус­тим, что Incubeast котируется по цене 20 долларов за акцию, т.е. следует купить 319,675 акции (6393,5 / 20). На самом деле мы не можем купить дробное число акций, поэтому купим либо 319, либо 320 акций. Следует также отметить, что не­большой лот из 19 или 20 акций, остающийся после покупки первых 300 акций, будет стоить дороже. Нестандартные, малые лоты обычно стоят несколько доро­же, поэтому мы переплатим за 19 или 20 акций, а это коснется ожидаемой прибы­ли по нашей позиции в Incubeast и в свою очередь затронет оптимальную комби­нацию портфеля. В некоторых случаях следует ограничиться только стандартным лотом (в на­шем случае — это 300 акций). Как видите, необходимо учитывать некоторый коэффициент ухудшения. Мы можем определить оптимальный портфель с точ­ностью до дробной части акции, но реальная торговля все равно внесет свои коррективы. Естественно, чем больше ваш счет, тем ближе будет реальный портфель к тео­ретическому. Допустим, вместо 50 000 долларов вы оперируете пятью миллиона­ми долларов. Вы хотите инвестировать 12,787% в Incubeast (если речь идет только об этих четырех инвестиционных альтернативах) и поэтому будете инвестиро­вать 5 000 000*0,12787 =$639 350. При цене 20 долларов за акцию вы бы ку­пили 639350/20=31967,5 акций. Учитывая круглый лот, вы купите 31900 акций, отклоняясь от оптимального значения примерно на 0,2%. Когда для инве­стирования у вас есть только 50 000 долларов, вы купите 300 акций вместо опти­мального количества 319,675 и таким образом отклонитесь от оптимального зна­чения примерно на 6,5%.

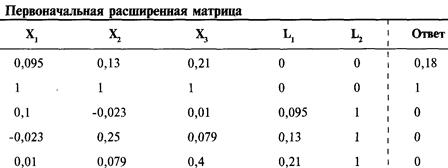
Подставим значения в уравнение (6.06a) (стр. 281):

Таким образом, при Е = 0,14 самое низкое значение V = 0,0725872809.

Если мы захотим протестировать значение Е = 0,18, то снова начнем с рас­ширенной матрицы, только на этот раз правая верхняя ячейка будет равна 0.18.

Xi		Xj		COVi, j
0,12391	*	0,12391	*	0,1	0,0015353688
0,12391	*	0,12787	*	-0,0237	-0,0003755116
0,12391	*	0,38407	*	0,01	0,0004759011
0,12391	*	0,36424	*
0,12787	*	0,12391	*	-0,0237	-0,0003755116
0,12787	*	0,12787	*	0,25	0,0040876842
0,12787	*	0,38407	*	0,079	0,0038797714
0,12787	*	0,36424	*
0,38407	*	0,12391	*	0,01	0,0004759011
0,38407	*	0,12787	*	0,079	0,0038797714
0,38407	*	0,38407	*	0,4	0,059003906
0,38407	*	0,36424	*
0,36424	*	0,12391	*
0,36424	*	0,12787	*
0,36424	*	0,38407	*
0,36424	*	0,36424	*
					0,0725872809

 

С помощью построчных операций получим единичную матрицу:

На этот раз в четвертой ячейке столбца ответов мы получили отрицательный ре­зультат. Это означает, что нам следует инвестировать отрицательную сумму в размере 9,81% капитала в сберегательный счет. Чтобы решить проблему отрица­тельного X_i (т.е. когда значение на пересечении строки i и крайнего правого столбца меньшее или равно нулю), мы должны удалить из первоначальной рас­ширенной матрицы строку i + 2 и столбец i и решить задачу для новой расши­ренной матрицы. Если значения последних двух строк крайнего правого столб­ца меньше или равны нулю, нам не о чем беспокоиться, поскольку они соответ­ствуют множителям Лагранжа и могут принимать отрицательные значения. Так как отрицательное значение переменной соответствует отрицательному весу четвертого компонента, мы удалим из первоначальной расширенной матрицы четвертый столбец и шестую строку. Затем используем построчные операции для проведения элементарных преобразований, чтобы получить единичную матрицу:

С помощью построчных операций получим единичную матрицу:

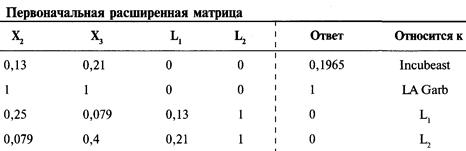
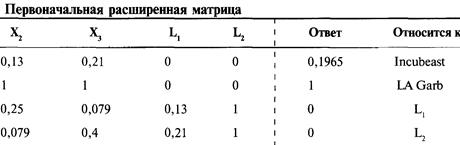
Когда вы удаляете строки и столбцы, важно помнить, какие строки каким пере­менным соответствуют, особенно когда таких строк и столбцов несколько. Допу­стим, нам надо найти веса в портфеле при Е = 0,1965. Единичная матрица, кото­рую мы сначала получим, будет содержать отрицательные значения для весов Toxico (X₁) и сберегательного счета (Х₄). Поэтому вернемся к нашей первоначаль­ной расширенной матрице:

Теперь удалим строку 3 и столбец 1 (они относятся к Toxico), а также удалим стро­ку 6 и столбец 4 (они относятся к сберегательному счету):

Итак, мы будем работать со следующей матрицей:

С помощью построчных операций получим единичную матрицу:

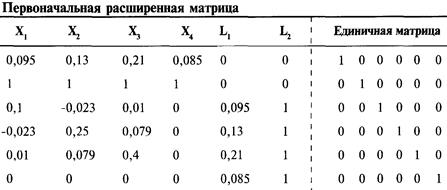
Решить матрицу можно также с помощью обратной матрицы коэффициентов. Обратная матрица при умножении на первоначальную матрицу дает единичную матрицу. В матричной алгебре матрица часто обозначается выделенной заглавной бук­вой. Например, мы можем обозначить матрицу коэффициентов буквой С. Обрат­ная матрица помечается верхним индексом -1. Обратная матрица к С обозначает­ся как С^-1.Чтобы использовать этот метод, необходимо определить обратную мат­рицу для матрицы коэффициентов. Для этого добавим к матрице коэффициентов единичную матрицу. В примере с 4 акциями:

Используя построчные операции, преобразуем матрицу коэффициентов в еди­ничную матрицу. Так как каждая построчная операция, проведенная слева, будет проведена и справа, мы преобразуем единичную матрицу справа в обратную мат­рицу С^-1.

Теперь мы можем умножить обратную матрицу С^-1 на первоначальный крайний правый столбец, который в нашем случае выглядит следующим образом:

При умножении матрицы на вектор-столбец мы умножаем все элементы первого столбца матрицы на первый элемент вектора, все элементы второго столбца матрицы на второй элемент вектора, и так далее. Если бы вектор был вектор-строка, мы бы умножили все элементы первой строки матрицы на первый элемент вектора, все элементы второй строки матрицы на второй элемент вектора, и так далее. Так как речь идет о векторе-столбце и после­дние четыре элемента нули, нам надо умножить первый столбец обратной матрицы на Е (ожидаемая прибыль портфеля) и второй столбец обратной матрицы на S (сумма весов). Мы получим следующий набор уравнений, в ко­торые можно подставить значения Е и S и получить оптимальные веса.

Матричная алгебра включает в себя гораздо больше тем и приложений, чем было рассмотрено в этой главе. Существуют и другие методы матричной алгебры для ре­шения систем линейных уравнений. Часто вы встретите ссылки на правило Краме­ра, симплекс-метод или симплексную таблицу. Эти методы сложнее, чем методы, описанные в этой главе. Существует множество применений матричной алгебры в бизнесе и науке, мы же затронули ее настолько, насколько необходимо для наших це­лей. Для более подробного изучения матричной алгебры и ее применений в бизнесе и науке рекомендую прочитать книгу «Множества, матрицы и линейное программи­рование» Роберта Л. Чилдресса (Sets, Matrices, and Linear Programming, by Robert L. Childress). Следующая глава посвящена методам, уже рассмотренным в этой главе, приме­нительно к любому торгуемому инструменту с использованием оптимального f и ме­ханических систем.