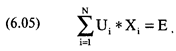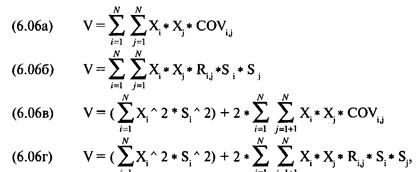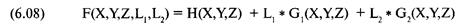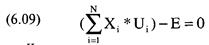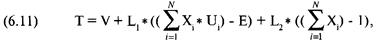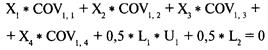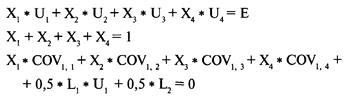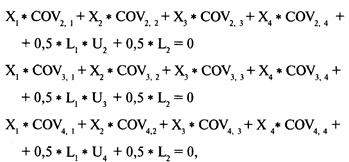Определение проблемы

На некоторое время оставим саму идею оптимального f (мы вернемся к нему поз­же). Легче всего понять параметрическое выведение эффективной границы, если рассмотреть портфель акций. Будем исходить из того, что эти акции находятся на денежном счете и полностью оплачены, т.е. они куплены не за счет кредита, полу­ченного от брокерской фирмы (не на маржинальном счете). С учетом этого ограничения мы выведем эффективную границу портфелей, т.е. из предложенных акций создадим комбинацию, которая будет иметь наименьший уровень ожидаемого риска для данного уровня ожидаемого выигрыша. Эти уровни задаются степенью неприятия риска инвестором. Теория Марковица (или Совре­менная теория портфеля) часто называется теорией Е— V (Expected return (ожида­емая прибыль) —Variance of return (дисперсия прибыли)). Отметьте, что входные параметры основаны на данных по прибыли, таким образом, входные данные для выведения эффективной границы — это прибыли, которые мы ожидаем по данной акции, и дисперсия, которая ожидается от этих прибылей. Прибыли по акциям оп­ределяются как дивиденды, ожидаемые за определенный период времени, плюс повышение рыночной стоимости акций (или минус уменьшение) за этот же пери­од, выраженные в процентах. Рассмотрим четыре потенциальные инвестиции, три из которых — в акции, а одна — в сберегательный счет с процентной ставкой 8 1/2% в год. Отметьте, что в этом примере продолжительность периода инвестирования (когда мы измеряем прибыли и их дисперсии) — 1 год:

 

Инвестиция Ожидаемая прибыль	Ожидаемая дисперсия прибыли
Toxico	9,5%	10%
Incubeast Corp.	13%	25%
LA Garb	21%	40%
Сберегательный счет	8,5%	0%

 

Если прибавить к значению ожидаемой прибыли единицу, мы получим HPR. Так­же мы можем извлечь квадратный корень из значения ожидаемой дисперсии при­были и получить ожидаемое стандартное отклонение прибыли.

Используемый временной горизонт не имеет значения при условии, что он одинаковый для всех рассматриваемых компонентов. Если речь идет о прибыли, неважно, что мы используем: год, квартал, 5 лет или день, — пока ожидаемые прибыли и стандартные отклонения для всех рассматриваемых компонентов име­ют одни и те же временные рамки.

 

Инвестиция	Ожидаемая прибыль (HPR)	Ожидаемое стандартное отклонение прибыли
Toxico	1,095	0,316227766
Incubeast Corp.	1,13	0,5
LA Garb	1,21	0,632455532
Сберегательный счет	1,085

 

Ожидаемая прибыль — это то же самое, что и потенциальная прибыль, а дисперсия (или стандартное отклонение) ожидаемых прибылей ~ то же самое, что и потен­циальный риск. Отметьте, что данная модель двумерная. Мы можем сказать, что модель представлена правым верхним квадрантом декартовой системы коорди­нат (см. рисунок 6-1), где по вертикали (ось Y) откладывается ожидаемая при­быль, а по горизонтали (ось X) откладывается ожидаемая дисперсия, или стандар­тное отклонение прибылей.

Рисунок 6-1 Правый верхний квадрант декартовой системы координат

 

Есть и другие аспекты потенциального риска, такие как потенциальный риск (ве­роятность) катастрофического убытка, который теория Е — V не рассматривает отдельно от дисперсии прибылей. Мы не будем изучать эту концепцию в данной главе, а будем обсуждать теорию Е — V в классическом варианте. Марковиц также утверждал, что портфель, полученный из теории Е — V, оптимален только в том случае, если полезность, т.е. «удовлетворение» инвестора, является лишь функци­ей ожидаемой прибыли и дисперсии ожидаемой прибыли. Марковиц указал, что инвестор может использовать и более высокие моменты распределения, а не только первые два (на которых основана теория Е — V), например асимметрию и эксцесс ожидаемых прибылей.

Потенциальный риск — очень емкое понятие, он является функцией гораз­до большего числа переменных и включает более высокие моменты распределе­ний. Тем не менее мы будем определять потенциальный риск как дисперсию ожидаемых прибылей. Не следует, однако, полагать, что этим риск полностью определен. Риск намного шире, и его реальная природа плохо поддается коли­чественной оценке.

Первое, что должен сделать инвестор, желающий использовать теорию Е — V, это придать количественный смысл своим предположениям относи­тельно ожидаемых прибылей и дисперсий прибылей рассматриваемых цен­ных бумаг на определенном временном горизонте (периоде удержания). Эти параметры можно получить эмпирически. Инвестор может рассмотреть про­шлую историю ценных бумаг и рассчитать прибыли и их дисперсии за опреде­ленные периоды. Как уже было отмечено, термин «прибыли» означает не толь­ко дивиденды по ценной бумаге, но и любые повышения стоимости ценной бумаги (в процентах). Дисперсия является статистической дисперсией про­центных прибылей. Для определения ожидаемой прибыли в период удержа­ния можно использовать линейную регрессию по прошлым прибылям. Дис­персия как входной параметр определяется путем расчета дисперсии каждой прошлой точки данных на основе ее спрогнозированного значения (а не на основе линии регрессии, рассчитанной для прогнозирования следующей ожидаемой прибыли). Вместо того чтобы определять эти значения эмпири­ческим способом, инвестор может оценить значения будущих прибылей и дисперсий1. Возможно, наилучшим способом нахождения параметров явля­ется комбинация обоих подходов. Инвестору следует использовать эмпири­ческий подход (т.е. использовать исторические данные), затем, если это необ­ходимо, можно учесть прогноз относительно будущих значений ожидаемых прибылей и дисперсий. Следующими параметрами, которые должен знать инвестор для использования данного метода, являются коэффициенты линейной корреляции прибылей. Эти параметры можно получить эмпирически, путем оценки или с помощью комби­нации обоих подходов.

При определении коэффициентов корреляции важно использовать точки данных того же временного периода, который был использован для определения ожидаемых прибылей и дисперсий. Другими словами, если вы используете годо­вые данные для определения ожидаемых прибылей и дисперсии прибылей (т.е. ведете расчеты на годовой основе), следует использовать годовые данные и при определении коэффициентов корреляции. Если вы используете дневные данные для определения ожидаемых прибьыей и дисперсии прибылей (т.е. ведете расче­ты на дневной основе), тогда вам следует использовать дневные данные для опре­деления коэффициентов корреляции. Вернемся к нашим четырем инвестициям — Toxico, Incubeast Corp., LA Garb и сберегательному счету. Присвоим им символы Т, 1, L и S соответственно. Ниже приведена таблица их коэффициентов линейной корреляции:

 

	I	L	S
Т	-0,15	0,05	о
I		0,25	о
L			о

 

На основе полученных параметров мы можем рассчитать ковариацию между дву­мя ценными бумагами:

Стандартные отклонения S_a и S_б можно найти, взяв квадратный корень диспер­сии ожидаемых прибылей для ценных бумаг а и б. Вернемся к нашему примеру. Мы можем определить ковариацию между Toxico (Т) и Incubeast (I) следующим образом:

Зная ковариацию и стандартные отклонения, мы можем рассчитать коэффици­ент линейной корреляции:

Отметьте, что ковариация ценной бумаги самой к себе является дисперсией, так как коэффициент линейной корреляции ценной бумаги самой к себе равен 1:

Теперь можно создать таблицу ковариаций для нашего примера с четырьмя инве­стиционными альтернативами:

 

	Т	I	L	S
Т	0,1	- 0,0237	0,01
I	- 0,0237	0,25	0,079
L	0,01	0,079	0,4
S

 

Мы собрали необходимую параметрическую информацию и теперь попытаемся сформулировать основную проблему. Во-первых, сумма весов ценных бумаг, со­ставляющих портфель, должна быть равна 1, так как операции ведутся на денеж­ном счете, и каждая ценная бумага полностью оплачена:

где N == число ценных бумаг, составляющих портфель;

Х = процентный вес ценной бумаги L

Важно отметить, что в уравнении (6.04) каждое значение Х должно быть неотрица­тельным числом.

Следующее равенство относится к ожидаемой прибыли всего портфеля — это Е в теории Е — V. Ожидаемая прибыль портфеля является суммой прибылей его компонентов, умноженных на соответствующие веса:

где Е = ожидаемая прибыль портфеля;

N = число ценных бумаг, составляющих портфель;

X_i = процентный вес ценной бумаги i;

U_i= ожидаемая прибыль ценной бумаги i. И наконец, мы подошли к параметру V, т. е дисперсии ожидаемых прибылей:

Нашей целью является поиск значений Х (причем их сумма равна единице), ко­торые дают наименьшее значение V для определенного значения Е. Максимизи­ровать (или минимизировать) функцию Н(Х, Y) при наличии условия или огра­ничения G(X, Y) можно с помощью метода Лагранжа. Для этого зададим функцию Лагранжа F(X, Y, L):

(6.07) F(X,Y,L) = H(X,Y) + L * G(X,Y)

Обратите внимание на форму уравнения (6.07). Новая функция F(X,Y,L) равна множителю Лагранжа L (его значение мы пока не знаем), умноженному на огра­ничительную функцию G(X,Y), плюс первоначальная функция H(X,Y), экстре­мум которой мы и хотим найти.

Решение этой системы из трех уравнений даст точки (X₁Y₁) относительного экстремума:

F_xX,Y,L) = О F_y(X,Y,L) = О F_L(X,Y,L) = О

Допустим, мы хотим максимизировать произведение двух чисел при условии, что их сумма равна 20. Пусть Х и Y два числа. Таким образом, H(X,Y) = Х * Y является функцией, которая должна быть максимизирована при нали­чии ограничительной функции G(X,Y) = Х + Y - 20 = 0. Зададим функцию Лагранжа:

F(X,Y,L) = Х * Y + L * (X + Y- 20) F_x(X,Y,L)=Y+L F_y(X,Y,L)=X+L F_L(X,Y,L)=

X +Y-20

Теперь приравняем F^(X,Y,L) и Fy(X,Y,L) нулю и решим каждое из них для полу­чения L:

Y+L=0 Y=-L и

X+L=0 X=-L

Теперь, приняв F_L(X,Y,L) = 0, мы получим Х + Y - 20 = 0. Наконец, заме­ним Х и Y эквивалентными выражениями, содержащими L:

(-L) + (-L) - 20 = О 2 * -L - 20 L=-10

Так как Y = -L, то Y = 10 и Х = 10. Максимальное произведение: 10*10= 100.

Метод множителей Лагранжа был продемонстрирован для двух переменных и одной 01раничительной функции. Метод можно также применять, когда есть бо­лее чем две переменные и более чем одна ограничительная функция. Далее для примера следует форма для поиска экстремума, когда есть три переменные и две ограничительные функции:

В этом случае, чтобы определить точки относительных экстремумов, вам надо ре­шить систему из пяти уравнений с пятью неизвестными. Позже мы покажем, как это сделать.

Сформулируем проблему несколько иначе: необходимо минимизировать V, т.е. дисперсию всего портфеля, с учетом двух следующих ограничений:

где N= число ценных бумаг, составляющих портфель;

Е = ожидаемая прибыль портфеля;

Х = процентный вес ценной бумаги i;

U. = ожидаемая прибыль ценной бумаги i.

Минимизация ограниченной функции многих переменных может быть проведе­на путем введения множителей Лагранжа и частного дифференцирования по каждой переменной. Поэтому мы сформулируем поставленную задачу в терминах функции Лагранжа, которую назовем Т:

где V= дисперсия ожидаемых прибылей портфеля из уравнения (6.06);

N = число ценных бумаг, составляющих портфель;

Е = ожидаемая прибыль портфеля;

X. = процентный вес ценной бумаги i;

U. = ожидаемая прибыль ценной бумаги i;

L, = первый множитель Лагранжа;

L = второй множитель Лагранжа.

Мы получим портфель с минимальной дисперсией (т.е. минимальным риском), приравняв к нулю частные производные функции Т по всем переменньм.

Давайте снова вернемся к нашим четырем инвестициям: Toxico, Incubeast Corp., LA Garb и сберегательному счету. Если мы возьмем первую частную произ­водную Т по Х₁, то получим:

Приравняв это выражение нулю и разделив обе части уравнения на 2, получим:

Таким же образом:

Таким образом, проблему минимизации V при данном Е для портфеля с N компонентами можно решить с помощью системы N + 2 уравнений с N + 2 неиз­вестными. Для случая с четырьмя компонентами обобщенная форма будет иметь следующий вид:

 

 

где Е = ожидаемая прибыль портфеля;

Х_i = процентный вес ценной бумаги i;

U_i = ожидаемая прибыль по ценной бумаге i;

COV _{А, Б} = ковариация между ценными бумагами А и Б;

L₁ = первый множитель Лагранжа;

1₂ = второй множитель Лагранжа.

Обобщенную форму можно использовать для любого числа компонентов. Напри­мер, если речь идет о трех компонентах (т.е. N = 3), система уравнений будет выг­лядеть следующим образом:

Прежде чем решать систему уравнений, необходимо задать уровень ожидаемой прибыли Е. Решением будет комбинация весов, которая даст искомое Е при наименьшей дисперсии. После того как вы определитесь с выбором Е, у вас бу­дут все входные переменные, необходимые для построения матрицы коэффи­циентов.

Переменная Е в правой части первого уравнения — это значение прибыли. для которой вы хотите определить комбинацию ценных бумаг в портфеле. Первое уравнение говорит о том, что сумма всех ожидаемых прибылей, умноженных на

соответствующие веса, должна равняться заданному Е. Второе уравнение отража­ет тот факт, что сумма весов должна быть равна 1. Была показана матрица для слу­чая с тремя ценными бумагами, но вы можете использовать обобщенную форму для N ценных бумаг.

Возьмем ожидаемые прибыли и ковариации из уже известной таблицы ковариаций и подставим коэффициенты в обобщенную форму. Таким образом из ко­эффициентов обобщенной формы можно создать матрицу. В случае четырех ком­понентов (N = 4) мы получим 6 рядов (N + 2):

 

X1	X2	X3	X4	L1	L2	Ответ
0,095	0,13	0,21	0,085			Е
0,1	- 0,0237	0,01		0,095
- 0,0237	0,25	0,079		0,13
0,01	0,079	0,4		0,21
				0,085

 

Отметьте, что мы получили 6 столбцов коэффициентов. Если добавить столбец свободных членов к матрице коэффициентов, мы получим расширенную матрицу.

Заметьте, что коэффициенты в матрице соответствуют нашей обобщенной форме:

Матрица является удобным представлением этих уравнений. Чтобы решить сис­тему уравнений, необходимо задать Е. Ответы, полученные при решении этой

системы уравнений, дадут оптимальные веса, минимизирующие дисперсию при­были всего портфеля для выбранного уровня Е.

Допустим, мы хотим найти решение для Е = 0,14, что соответствует прибыли в 14%. Подставив в матрицу 0,14 для Е и нули для переменных L₁ и L₂ в первых двух строках, мы получим следующую матрицу:

X1	X2	Х3	X4	L1	L2	Ответ
0,095	0,13	0,21	0,085			0,14
0,1	- 0,0237	0,01		0,095
- 0,0237	0,25	0,079		0,13
0,01	0,079	0,4		0,21
				0,085

 

Необходимо найти N + 2 неизвестных с помощью N + 2 уравнений.