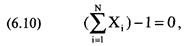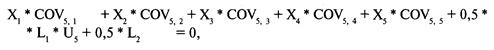Неограниченные портфели
В этом разделе мы увидим, что можно поднять прибыли выше линии GCML, если снять ограничение на сумму весов. Давайте вернемся к геометрическим оптимальным портфелям. Если мы попробуем составить геометрический оптимальный портфель из наших четырех рыночных систем — Toxico, Incubeast, LA Garb и сберегательного счета, то с помощью уравнений с (7.0ба) по (7.06г) найдем, что он является таковым при Е, равном 0,1688965, и V, равном 0,1688965. Среднее геометрическое такого портфеля будет равно 1,094268, а состав портфеля будет иметь вид: Toxico 18,89891% Incubeast 19,50386% LA Garb 58,58387% Сберегательный счет 0,03014% При решении уравнений с (7.06а) по (7.06г) необходимо использовать метод итераций, т.е. выбирать тестируемое значение для Е и решать матрицу для этого Е. Если полученное значение дисперсии больше значения Е, это означает, что тестируемое значение Е слишком высокое и в следующей попытке следует его понизить. Вы можете определить дисперсию портфеля, используя одно из уравнений с (6.06а) по (6.06г). Повторяйте процесс, пока не будет выполняться любое из равенств с (7.06а) по (7.06г). Таким образом вы получите геометрический оптимальный портфель (отметьте, что все рассмотренные портфели на эффективной границе AHPR или на эффективной границе GHPR определяются с учетом того, что сумма весов равна 100%, или 1,00). Вспомните уравнение (6.10), используемое в первоначальной расширенной матрице для поиска оптимальных весов портфеля, уравнение отражает тот факт, что сумма весов равна 1:
где N = количество ценных бумаг, составляющих портфель; X. = процентный вес ценной бумаги L Уравнение также можно представить следующим образом:
Мы можем найти неограниченный оптимальный портфель, если левую часть этого уравнения приравнять к числу больше 1. Для этого добавим еще одну рыночную систему, называемую беспроцентным вкладом (non-interest-bearing cash (NIC)), в первоначальную расширенную матрицу Данная рыночная система будет иметь дневное среднее арифметическое HPR= 1,0, а стандартное отклонение, дисперсию и ковариацию дневных HPR равными 0. Коэффициенты корреляции NIC с любой другой рыночной системой всегда равны 0. Теперь установим ограничение суммы весов на некоторое произвольное число, большее единицы. Хорошим первоначальным значением будет количество используемых рыночных систем (без NIC), умноженное на три. Так как мы имеем 4 рыночные системы (не учитывая NIC), то ограничим сумму весов 4*3=12. Отметьте, что мы просто устанавливаем ограничение на произвольное значение, большее единицы. Разность между этим выбранным значением и суммой полученных весов будет весом системы NIC. На самом деле, мы не собираемся инвестировать в NIC. Это просто дополнительная переменная, с помощью которой мы создадим матрицу для получения неограниченных весов рыночных систем. Теперь возьмем параметры наших четырех рыночных систем из главы 6 и добавим NIC:
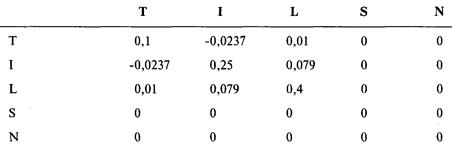
Ковариации рыночных систем, включая NIC, будут следующими:
Добавив NIC, мы получим 5 рыночных систем, и обобщенная форма первоначальной расширенной матрицы будет выглядеть следующим образом:
неограниченных весов рыночных систем. Теперь возьмем параметры наших четырех рыночных систем из главы 6 и добавим NIC:
Ковариации рыночных систем, включая NIC, будут следующими:
Добавив NIC, мы получим 5 рыночных систем, и обобщенная форма первоначальной расширенной матрицы будет выглядеть следующим образом:
После включения NIC первоначальная расширенная матрица приобретет вид:
Отметьте, что значение на пересечении столбца ответов и второй строки, т.е. ограничение суммы весов, равно количеству рыночных систем (не включая NIC), умноженному на 3. С помощью элементарных преобразований, описанных в главе 6, получим единичную матрицу. Теперь вы можете определить эффективную границу AHPR и эффективную границу GHPR для портфеля с неограниченными весами. Эффективная граница AHPR для портфеля с неограниченными весами соответствует использованию рычага (заемного капитала) без реинвестирования. Эффективная граница GHPR соответствует использованию рычага и реинвестированию прибылей. Наша цель — найти оптимальный неограниченный геометрический портфель, который в результате даст наибольший геометрический рост. Можно использовать уравнения с (7.Оба) по (7.06г) для нахождения на эффективной границе геометрического оптимального портфеля. В нашем случае, независимо от того, какое значение мы пытаемся найти для Е (значение на пересечение столбца ответов и первой строки), мы получаем один и тот же портфель, состоящий только из сберегательного счета, поднятого рычагом для достижения желаемого значения Е. В этом случае мы получаем самое низкое V (т. е. 0) для любого Е. Удалим из матрицы сберегательный счет и повторим процедуру. На этот раз мы рассмотрим только четыре рыночные системы (Toxico, Incubeast, LA Garb и NIC) и ограничим сумму весов числом 9. Мы должны поступить таким образом, потому что, как только в матрице появляется компонент с нулевой дисперсией и AHPR большим 1, мы получаем оптимальный портфель, состоящий из одного компонента, а для соответствия требуемому Е будет меняться только рычаг этого компонента. Решив матрицу, мы увидим, что уравнения с (7.06а) по (7.06г) удовлетворяются при Е, равном 0,2457. Так как это геометрический оптимальный портфель, V также равно 0,2457. Получившееся среднее геометрическое равно 1,142833. Портфель будет выглядеть следующим образом: Toxico 102,5982% Incubeast 49,00558% LA Garb 40,24979% NIC 708,14643% Возникает резонный вопрос: «Каким образом сумма весов компонентов может быть больше 100%?» Мы ответим на этот вопрос, но несколько позже. Если NIC не является одним из компонентов геометрического оптимального портфеля, то следует поднять ограничение суммы весов S до уровня, когда NIC станет одним из компонентов геометрического оптимального портфеля. Вспомните, что если в портфеле есть только два компонента, причем коэффициент корреляции между ними равен -1 и оба компонента имеют положительное математическое ожидание, тогда от вас потребуется финансирование бесконечного числа контрактов, поскольку такой портфель никогда не будет проигрывать. Следует также отметить, что чем ниже коэффициенты корреляции между компонентами в портфеле, тем выше процент, требуемый для инвестирования в эти компоненты. Разность между инвестированными процентными долями и ограничением суммы весов S должна быть заполнена NIC. Если NIC отсутствует среди компонентов геометрического оптимального портфеля, значит портфель работает при ограниченном S и поэтому не может считаться неограниченным геометрическим оптимальным портфелем. Так как вы не будете в действительности инвестировать в NIC, то не имеет значения, каков его вес, пока он является частью геометрического оптимального портфеля.
|