Если целевая функция одной из взаимо двойственных задач не ограничена, то

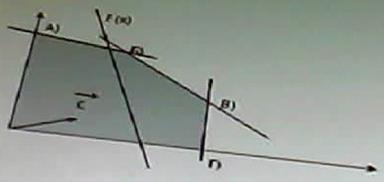
а) в другой задаче целевая функция тоже не ограничена;
б) другая задача не имеет решения;
в) другая задача имеет единственное решение.

Если Х* оптимальный план исходной (прямой) задачи с целевой функцией f(x)= 6х1+4х2, а y – оптимальный план двойственной к ней с целевой функцией F(y) = 20у1+40у2+25у3, то пара оптимальных планов:

а) Х*= (25;20) Y*= (3;6;4)

б) Х*= (20;25) Y*= (2;2;4) ДА

в) Х*= (22;10) Y*= (4;5;6)

г) Х*= (21;23) Y*= (3;5;6)

Если х1, х2,х3, х4 булевы переменные то условие выбора любых двух вариантов из четырех возможных, запишется в виде:

х1+ х2+х3 +х4 =2

Если х1, х2,х3, х4 булевы переменные то условие выбора по крайней мере одного вариантов, запишется в виде

х1+ х2+х3 +х4 =1

Если в исходной задаче неизвестная Х1= 9/2, то решая ее методом ветвей и границ, новые подзадачи образуются ограничениями:

а) первая подзадача будет содержать условия исходной задачи и дополнительное ограничение Х1 ≤ 4, а вторая подзадача образуется ограничением Х1 ≥ 5

Если задача ЦЛО решается методом ветвей и границ на максимум функции и в первой подзадаче f1max = 2500,25; а во второй f2max = 1900,75. Какую из подзадач при продолжении решения необходимо ветвить дальше?

первую

Задача ЦЛО решается методом ветвей и границ на максимум функции и в первой подзадаче f1max = 361,36; а во второй f2max = 450,93. Какую из подзадач при продолжении решения необходимо ветвить дальше?

первую

Задачи исследования операций в экономике это:

оптимизации цели системы при ограничениях на множество допустимых состояний системы

Задача линейной оптимизации называется вырожденной, если:

а) в столбце свободных членов симплексной таблицы имеется по крайней мере один нулевой элемент;

б) в столбце свободных членов симплексной таблицы все элементы положительные;

в) если в симплексной таблице имеются нулевые элементы.

3а разрешающий столбец при нахождении максимума целевой функции задачи линейной оптимизации выбирается тот:

а) в котором находится наименьший отрицательный элемент строки функции, за исключением элемента, находящегося в столбце свободных членов (ДА)

б) в котором находится отрицательный элемент строки функции;

в) в котором все элементы неотрицательные. НЕТ

Задача целочисленного линейного программирования переменные:

Принимают целые значения, ограниченные сверху

Задачи решаемые методом математического программирования являются:

а) любой класс задач

б) класс экстремальных задач

в) класс задач на экстремум (максимум или минимум) функции со многими неизвестными ДА

Задачей нелинейного программирования является задача, у которой:

а) нелинейной является целевая функция

б) некоторые или все ограничения являются нелинейными

в) функция и ограничения являются нелинейными

г) выполняется хотя бы одно из условий а, б или в

Задача линейного программирования на максимум решается графическим методом. Укажите точку, в которой целевая функция достигает своего максимального значения.

а) А (НЕТ)

б) Б???

в) В

г) Г

Задача нелинейного программирования с ограничениями неравенствами может быть решена методом множителей Лагранжа если:

ограничения неравенства привести к равенствам и наложить условие неотрицательности на дополнительные переменные.