АDCD – область допустимых значений.
а) А ДА б) В в) С г) D Определить в какой точке находится максимальное значение ЗЛП решая графическим способом.
ABCDE – область допустимых значений. а) А б) B в) С ДА г) D д) E Определите разрешающий элемент в следующей симплексной таблице при решении задачи максимизации:
Определить будет ли данный план опорным, если нет, то почему: Изображена таблица а) будет НЕТ б) не будет, т.к. не все клетки заполнены в) не будет, т.к. не выполняется условие m+n-1 НЕТ г) не будет, т.к. для некоторых занятых клеток … Особенностью задач динамического программирования заключается в том, что: дальнейшее состояние экономической системы зависит только от данного состояния и не зависит от предыстории данного состояния Основные функциональные уравнения задачи оптимального распределения капиталовложений имеют: а) fN(c) = qN(c) fn(c) = max {qn (x) + fn-1 (c-x)} ДА б) fN(c) = qN(c) fn(c) = min {qn (x) + fn-1 (c-x)} в) fN(c) = qN(c) fn(c) = min {qn (x) + fn-1 (х-с)} Оцените целесообразность включения в план нового вида продукции, нормы затрат ресурсов на единицу которого равны соответственно 3, 4, 2, а прибыль от реализации равна 40 ден.ед., если при решении задачи о производстве продукции при оптимальном использовании ресурсов было получено следующее решение
Оцените целесообразность закупки 10 единиц второго вида ресурса по цене 2,5 ден.ед., если при решении задачи о производстве продукции при оптимальном использовании ресурсов было получено следующее решение
Оптимальной стратегией замены оборудования для оборудования возраста 4 года является:
а) 1 год f5(4) –замена; 2 год f4(1) –сохранение; 3 год f3(0) –сохранение; 4 год f2(1) –сохранение; 5 год f1(2) –сохранение. ДА б) 1 год f1(4) –сохранение; 2 год f2(3) –замена; 3 год f3(1) –сохранение; 4 год f4(2) –сохранение; 5 год f5(3) –замена. НЕТ в) 1 год f5(4) –замена; 2 год f4(1) –сохранение; 3 год f3(2) –сохранение; 4 год f2(3) –замена; 5 год f1(1) –сохранение. г) 1 год f1(4) –сохранение; 2 год f2(3) –замена; 3 год f3(0) –сохранение; 4 год f4(1) –сохранение; 5 год f5(2) –сохранение. д) 1 год f5(4) –замена; 2 год f4(0) –сохранение; 3 год f3(1) –сохранение; 4 год f2(2) –сохранение; 5 год f1(3) –сохранение. При решении нелинейных задач командой Поиск решения Excel значение функции в начальной точке должно быть: отлично от нуля, так как на каждом шаге итерационного процесса решения задачи проверяется достижение оптимального решения по формуле ∆f=fk+1 – fk / fk ≤ ε – заданная величина точности решения, а на нуль делить нельзя При решении задачи динамического программирования: а) она разбивается на шаги и процесс решения является ассоциативным; б) строится характеристический многочлен; в) процесс решения не является многошаговым; г) она разбивается на шаги и нумерация шагов (этапов) осуществляется от конечного этапа к начальному; (ДА) д) необходимо сложить значения переменных для каждого этапа. При решении задачи транспортного типа на максимум были получены оценки свободных клеток В=1,0 следовательно: Задача имеет …..ственное оптимальное решение ДА План находящийся в данной таблице является
По данному опорному плану определить транспортные расходы:
а) 215 ДА б) 230 в) 200 г) 254 д) 190 После приведения математической модели задачи линейной оптимизации к каноническому виду мы получаем: F = 6x1 -3x2 +7x3 (min)
x1≥0, x3≥0
Переход к нехудшему опорному решению транспортной задачи можно осуществить: а) методом потенциалов; б) методом северо-западного угла; в) методом наименьших квадратов; г) методом функциональных уравнений. Принцип оптимальности Беллмана для задачи в которой решается вопрос о том, как спланировать работу группы предприятий, чтобы экономический эффект от выделенных этим предприятиям дополнительных финансовых или материальных ресурсов был максимальным, формализуется в следующее функциональное уравнение динамического программирования. 1) 2) fn(t)= max 3) fn(xn-1, un) = min (zn(xn-1, un)+fn-1(xn)) При решении пары двойственных задач (одна из которых задача об оптимальном использовании ресурсов) получен следующий результат: f(
Полученный план перевозок транспортной задачи является
|



 ) = 5x1+3x2+x3 (max)
) = 5x1+3x2+x3 (max)
 (5; 0; 24; 4; 0; 0)
(5; 0; 24; 4; 0; 0)
 (0; 9; 3; 0; 2; 0).
(0; 9; 3; 0; 2; 0).
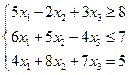
 xj≥0, (j=
xj≥0, (j=  )
)
 ) -7x3 (max)
) -7x3 (max)
 x1≥0, xj≥0, (j=
x1≥0, xj≥0, (j=  ), x
), x  ≥0,
≥0, 
 xj≥0, (j=
xj≥0, (j=  )
)
 (ДА)
(ДА)
 ) = 20x1+10x2+9x3 (max);
) = 20x1+10x2+9x3 (max);  =(2; 0; 4; 0; 5; 0). Значение прибыли, если в производство ввести 3 единицы наиболее дефицитного ресурса, будет равно
=(2; 0; 4; 0; 5; 0). Значение прибыли, если в производство ввести 3 единицы наиболее дефицитного ресурса, будет равно


