Допустимое решение транспортной задачи является опорным, если

а) в этом решении заполненные клетки таблицы транспортной задачи не образуют ни одного цикла (число заполненных клеток таблицы равно (m+n-1), где m- число
поставщиков, а n- число потребителей);
б) оно получено симплексным методом;
в) в этом решении заполненные клетки таблицы транспортной задачи образуют
циклы (число заполненных клеток таблицы равно (m+n+1), где m- число
поставщиков, а n- число потребителей).

Для прямой задачи min z =2х1+x3 x1+x2<=10 1<=x2<=5 x3<=10
двойственная задача имеет вид:

Для решения задач динамического программирования используется:

функционально- рекуррентное соотношение Р Беллмана

Для решения задачи сетевого планирования:

Матрица инцидентностей графа

Для следующей транспортной таблицы если значение потенциала U₁= -5, то значение потенциала U_? будет равно:

	В1(65)	В2(35)	В3(20)	В4(15)
А1(27)	6 2	21 3
А2(35)		14 6	20 1	1 3
А3(14)				14 1
А4(59)	59 4

а) -2 НЕТ

б) -3 ДА

в) 5

г) 10

Для следующей транспортной таблицы если значение потенциала V1 = 7, то ……

а) 2 НЕТ

б) – 2

в) 0

г) 7

Для следующей транспортной таблицы оценка свободной клетки (1; 3) равна:

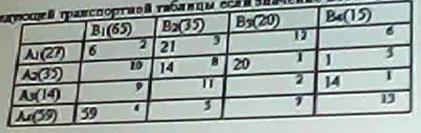
-9

6 (НЕТ)

Для данного опорного плана транспортной задачи по критерию стоимости значение целевой функции будет равно:

	В1(65)	В2(35)	В3(20)	В4(15)
А1(27)	6 2	21 3
А2(35)		14 6	20 1	1 3
А3(14)				14 1
А4(59)	59 4

а) 136 (или 196)

б) 24 НЕТ

в) 432 (ДА)

г) 462 (тогда этот ответ, если я где-то ошибся в цифрах таблицы

Для решения задачи коммивояжера используется:

Матрица смежностей графа

Для решения задач линейной оптимизации можно использовать следующий математический аппарат:

а) графический метод;

б) симплексный метод;

в) метод наименьших квадратов;

г) метод аппроксимации;

д) асимптотические формулы.

Для нахождения решения двойственной задачи необходимо воспользоваться:

а) оптимальным решением (последняя симплексная таблица) исходной задачи и соответствием между переменными прямой и двойственной задач; ДА

б) первой симплексной таблицей исходной задачи;

в) значениями целевых функций двойственных задач;

г) дополнительными переменными исходной задачи.

Для решения задачи о назначениях используется:

Матрица смежностей графа

Для решения задач линейной целочисленной оптимизации применяют метод:

Гомори

Ветвей и границ

Для решения параметрических задач линейного программирования используют:

Последовательную фиксацию переменного параметра с дальнейшим решением по схемам линейного программирования

Для данного опорного плана транспортной задачи по критерию стоимости значений целевой функции будет равен:

	В1(65)	В2(35)	В3(20)	В4(15)
А1(27)	6 5	21 2
А2(35)		14 4	20 4	1 4
А3(14)				14 2
А4(59)	59 1

а) 765

б) 299 ДА

в) 960

г) 375

Для данного опорного плана, находящегося в следующей таблице, значение функции будет равно

6   7   2   8   0     4   10   5   3   0     8   9   12   11   0

1) 1050; 2) 990; 3) 850; 4) 1070. (ДА)

 

Если в исходной (прямой) задаче линейного программирования целевая функция максимизируется, то в двойственной к ней целевая функция:

а) минимизируется ДА

б) максимизируется

в) может как максимизироваться так и минимизироваться

Если в исходной (прямой) задаче линейного программирования целевая функция минимизируется, то в двойственной к ней целевая функция:

а) минимизируется

б) максимизируется ДА

в) может как максимизироваться так и минимизироваться

Если в исходной (прямой) задаче линейного программирования на какую-то ……

а) записывается в виде неравенства

б) может быть как уравнением так и неравенством

в) в модель двойственной задачи не включается

г) записывается в виде уравнения ДА

Если в задаче на min все оценки Sij свободных клеток ≥ 0, то:

а) план оптимален ДА

б) плане не оптимален

в) план является опорным

г) план является начальным

Если в опорном решении транспортной задачи число отличных от нуля неизвестных равно m+n-1, то решение называется:

а) вырожденным;
б) невырожденным

Если в транспортной задаче суммарный запас груза у поставщиков больше суммарного спроса потребителей, то:

а) необходимо уменьшить спросы потребителей;
б) для разрешимости задачи необходимо вести фиктивного потребителя;
в) задача не имеет решения;
г) для разрешимости задачи необходимо вести фиктивного поставщика.

Если X* - оптимальный план исходной (прямой) задачи с ……….. f(x) 5X1 + 7X2; а y* - оптимальный план двойственной к ней с целевой функцией F(y) = 20у1 + 40у2 + 25у2, то пара……..

вариант В (НЕТ)

Если в транспортной задаче суммарный запас груза у поставщиков меньше суммарного спроса потребителей, то:

а) задача не имеет решения;

б) для разрешимости задачи необходимо ввести фиктивного поставщика;

в) для разрешимости задачи необходимо ввести фиктивного потребителя;

г) необходимо уменьшить опросы потребителей.

Если в f-строке симплексной таблицы задачи линейного программирования есть отрицательный элемент, которому соответствует столбец, не содержащий ни одного положительного элемента, то:

а) целевая функция непрерывная;
б) целевая функция неограниченна;
в) задача имеет бесконечное множество оптимальных планов.

Если в строке симплексной таблицы задачи линейной оптимизации есть отрицательный элемент и все элементы столбца, в котором он находится, неположительные, то:

а) целевая функция неограничена;

б) целевая функция четная;

в) целевая функция непрерывная.

Если в f-строке симплексной таблицы, содержащей оптимальный план, есть хотя бы один нулевой элемент, то:

а) задача имеет единственное решение;
б) задача не имеет решения;
в) решение задачи не завершено;
г) задача имеет множество оптимальных решений

Если число отличных от нуля объемов перевозок в решении транспортной задачи равно т+ п-1, то это решение называют:

а) вырожденным;

б) невырожденным;

в) открытым;

г) закрытым.

Если значение потенциала U₂ = 1, то значение потенциала V₃ будет равно

5   4   1   3     3   7   2   8     2   6   4   5

1) 6; 2) 5; 3) 0; 4) -2; 5) 3. (ДА)

 

Если найдено опорное решение транспортной задачи:

а) то для каждой свободной клетки этого решения можно образовать единственный цикл;

б) то для каждой свободной клетки можно образовать множество циклов;

в) то для каждой занятой клетки можно образовать единственный цикл.

Если в строке оптимального решения задачи линейной оптимизации есть хотя бы один нулевой элемент, то:

а) задача имеет множество оптимальных решений;

б) задача не имеет решений;

в) задача имеет единственное решение;

г) решение задачи не завершено.