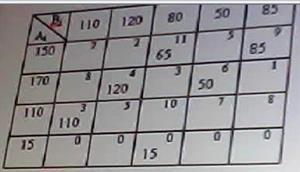
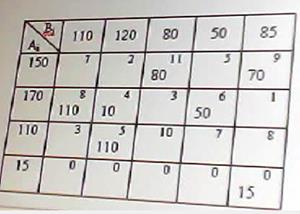
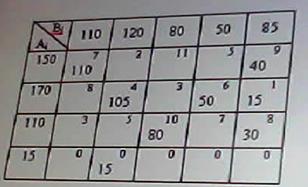
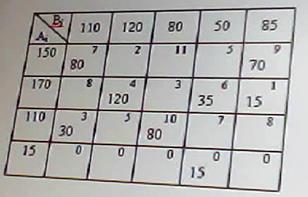
В чем заключается ограниченность применения графического метода решения задач нелинейного программирования?
позволяет решать задачи с ограниченным числом неизвестных (как правило с двумя неизвестными величинами) В задаче о распределении ограниченных ресурсов: Если ресурс израсходован полностью, то соответствующая двойственная переменная больше нуля Если ресурс не израсходован, то соответствующая двойственная переменная равна нулю В какой из транспортных таблиц содержится опорный план: А) Б) В) Г) А Б В НЕТ Г Верно ли, что оптимальным планом или оптимальным решением задачи линейного программирования называется план, доставляющий наименьшее (наибольшее) значение линейной функции. а) нет; В математическом программировании рассматриваются задачи: а) линейной оптимизации; б) нелинейной оптимизации; в) целочисленной оптимизации; г) динамического программирования; д) стохастической оптимизации; е) все задачи, перечисленные в пунктах а), б), в), г) и д). Выберете из следующих утверждений правильное: а) область допустимых решений задачи линейной оптимизаций всегда ограничена; б) область допустимых решений задачи линейной оптимизации всегда выпукла; в) область допустимых решений задачи линейной оптимизации может состоять из нескольких разрозненных областей. В задачах нелинейной оптимизации: возможны любые из вариантов перечисленных выше В задачах нелинейной оптимизации экстремальное значение целевой функции: возможны любые из перечисленных вариантов В рассмотренной модели транспортной задачи предполагается перевозка: а) однородного продукта; б) разнородных продуктов; в) разнородных комплектов; г) всевозможных материалов. В ограничениях линейных задач оптимального использования ограниченных ресурсов дополнительные (балансовые) переменные означают: а) величины неиспользованных ресурсов; б) убыток, получаемый от использования ресурсов; в) оценку дефицитности ресурсов; г) количество ресурсов. В ограничениях линейных задач оптимального составления рациона дополнительные (балансовые) переменные показывают: а) недостаточное потребление соответствующего компонента; б) оценку дефицитности компонента; в) цену компонента; г) количество компонента; д) потребление соответствующего компонента сверх нормы. Величина двойственной оценки задачи линейной оптимизации численно равна: а) величине изменения значения целевой функции при изменении соответствующего ресурса на единицу; б) значению свободной переменной; в) оптимальному объему выпускаемой продукций. В задаче параметрического линейного программирования: могут выполняться оба условия в) и г) Все вычисления, дающие возможность найти оптимальное значение эффекта, достигаемого за п шагов в задаче динамического программирования: а) производятся на основании основного функционального уравнения или рекуррентного соотношения; б) производятся на основании обыкновенных жордановых исключений; в) производятся на основании метода прямого воздействия.
|