Плоскости частного положения
Плоскости, параллельные плоскостям проекций, называют плоскостями уровня. Плоскость, параллельную плоскости проекций П1, называют горизонтальной (рисунок 2.26). Плоскость, параллельную плоскости проекций П2, называют фронтальной (рисунок 2.27). Плоскость, параллельную плоскости проекций П3, называют профильной (рисунок 2.28).
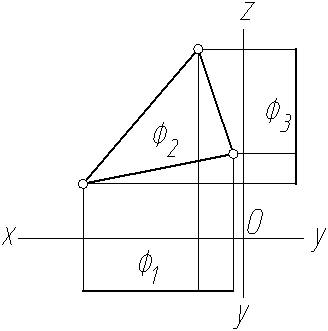
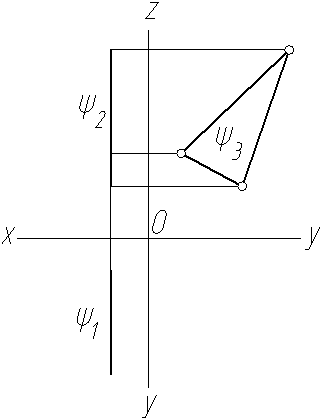
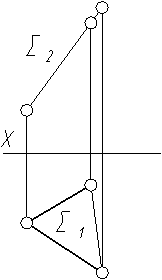
Например, горизонтальная плоскость Г, заданная отсеком (рисунок 2.26), проецируется на плоскость проекций П2в прямую линию Г2, перпендикулярную вертикальным линиям связи, а на плоскость проекций П3 – в прямую Г3, совпадающую с горизонтальной линией связи. На плоскость проекций П1 отсек проецируется в натуральную величину. Плоскости, перпендикулярные только одной плоскости проекций, называют проецирующими. Плоскость, перпендикулярную горизонтальной плоскости проекций П1, называют горизонтально проецирующей (рисунок 2.30). Плоскость, перпендикулярнуюфронтальной плоскости проекций П2, называют фронтально проецирующей (рисунок 2.31). Плоскость, перпендикулярную только профильной плоскости проекций П3, называют профильно проецирующей (рисунок 2.29).
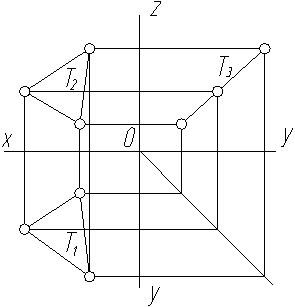
* В прямоугольной аксонометрии также рассматривается треугольник следов плоскости. При рассмотрении следов плоскости на комплексном чертеже не следует путать со следами в аксонометрических проекциях.
|