Пусть подынтегральная функция содержит квадратный трехчлен  .
.
1. Интегралы вида  вычисляются следующим образом. Из квадратного трехчлена в знаменателе выделим полный квадрат:
вычисляются следующим образом. Из квадратного трехчлена в знаменателе выделим полный квадрат:
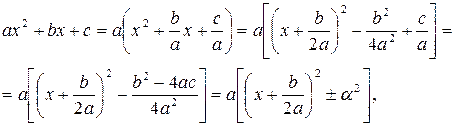
где  , если
, если 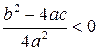 и
и  , если
, если  .
.
Далее сделаем подстановку  , откуда
, откуда  ,
,  . Получим
. Получим
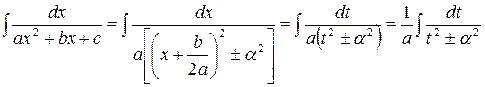 .
.
Последний интеграл является табличным и вычисляется по формулам 15, 16 таблицы основных неопределенных интегралов.
Пример 1. Вычислить интеграл  .
.
Решение. Выделим в знаменателе полный квадрат:

 .
.
Сделаем подстановку  . Тогда
. Тогда  и
и

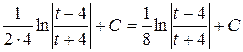 .
.
Возвращаясь к переменной х, получим
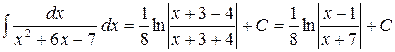 .
.
2. Интегралы вида  вычисляются аналогично интегралам пункта 1 путем выделения полного квадрата из квадратного трехчлена и последующей замены переменной. В результате исходный интеграл сводится к одному из табличных интегралов вида 12, 13.
вычисляются аналогично интегралам пункта 1 путем выделения полного квадрата из квадратного трехчлена и последующей замены переменной. В результате исходный интеграл сводится к одному из табличных интегралов вида 12, 13.
Пример 2. Вычислить интеграл  .
.
Решение. Преобразуем квадратный трехчлен следующим образом: 
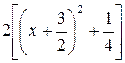 . Получим
. Получим  . Положим
. Положим  , тогда
, тогда  ,
,  . В результате получаем
. В результате получаем 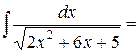
=  . Переходя к переменной х, получим
. Переходя к переменной х, получим
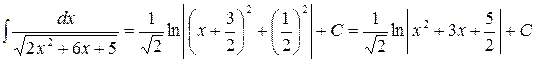 .
.
3. Интегралы вида  и
и  вычисляются путем выделения полного квадрата из квадратного трехчлена и последующей замены переменной. Затем полученный интеграл разбивается на два: первый из этих интегралов можно вычислить, воспользовавшись формулами (2), (3), а второй интеграл является табличным.
вычисляются путем выделения полного квадрата из квадратного трехчлена и последующей замены переменной. Затем полученный интеграл разбивается на два: первый из этих интегралов можно вычислить, воспользовавшись формулами (2), (3), а второй интеграл является табличным.
Пример 3. Вычислить интеграл  .
.
Решение. Так как  , то по-ложим
, то по-ложим  . Тогда
. Тогда  и
и  = [полученный интеграл разобьем на два] =
= [полученный интеграл разобьем на два] =  . Второй из этих ин-тегралов – табличный:
. Второй из этих ин-тегралов – табличный: 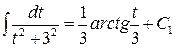 . Для нахождения первого воспользуемся следующим преобразованием дифференциала:
. Для нахождения первого воспользуемся следующим преобразованием дифференциала:  . В результате получим
. В результате получим 
 = [воспользуемся формулой (3)] =
= [воспользуемся формулой (3)] =  . Окончательно имеем
. Окончательно имеем 
 , где
, где  . Возвращаясь к переменной х, получим
. Возвращаясь к переменной х, получим

 .
.

 .
. вычисляются следующим образом. Из квадратного трехчлена в знаменателе выделим полный квадрат:
вычисляются следующим образом. Из квадратного трехчлена в знаменателе выделим полный квадрат: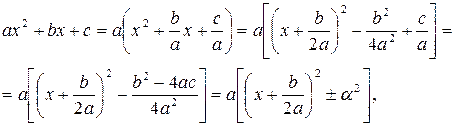
 , если
, если 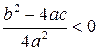 и
и  , если
, если  .
. , откуда
, откуда  ,
,  . Получим
. Получим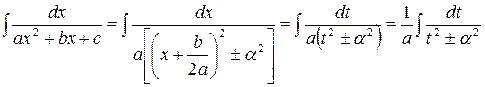 .
. .
.
 .
. . Тогда
. Тогда  и
и
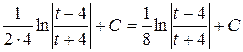 .
.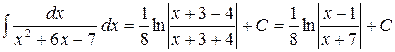 .
. вычисляются аналогично интегралам пункта 1 путем выделения полного квадрата из квадратного трехчлена и последующей замены переменной. В результате исходный интеграл сводится к одному из табличных интегралов вида 12, 13.
вычисляются аналогично интегралам пункта 1 путем выделения полного квадрата из квадратного трехчлена и последующей замены переменной. В результате исходный интеграл сводится к одному из табличных интегралов вида 12, 13. .
.
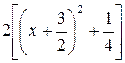 . Получим
. Получим  . Положим
. Положим  , тогда
, тогда  ,
, 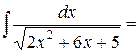
 . Переходя к переменной х, получим
. Переходя к переменной х, получим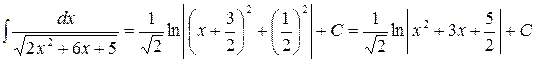 .
. и
и  вычисляются путем выделения полного квадрата из квадратного трехчлена и последующей замены переменной. Затем полученный интеграл разбивается на два: первый из этих интегралов можно вычислить, воспользовавшись формулами (2), (3), а второй интеграл является табличным.
вычисляются путем выделения полного квадрата из квадратного трехчлена и последующей замены переменной. Затем полученный интеграл разбивается на два: первый из этих интегралов можно вычислить, воспользовавшись формулами (2), (3), а второй интеграл является табличным. .
. , то по-ложим
, то по-ложим  . Тогда
. Тогда  и
и  = [полученный интеграл разобьем на два] =
= [полученный интеграл разобьем на два] =  . Второй из этих ин-тегралов – табличный:
. Второй из этих ин-тегралов – табличный: 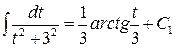 . Для нахождения первого воспользуемся следующим преобразованием дифференциала:
. Для нахождения первого воспользуемся следующим преобразованием дифференциала:  . В результате получим
. В результате получим 
 = [воспользуемся формулой (3)] =
= [воспользуемся формулой (3)] =  . Окончательно имеем
. Окончательно имеем 
 , где
, где  . Возвращаясь к переменной х, получим
. Возвращаясь к переменной х, получим
 .
.


