Лекция 1
1. а) в) д) ж)
2. а) в) д) ж) и) л) 3. a) в) д) ж) и)
Лекция 2 1. а) в) д) ж) и) к) л) м)
2. а) в) д)
3. а) в) д) ж) и) л) СОДЕРЖАНИЕ
Лекция 1. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ............................................................. 3 1. Понятие первообразной функции. Неопределенный интеграл... 3 2. Основные свойства неопределенного интеграла......................... 5 3. Таблица основных неопределенных интегралов......................... 5 4. Основные методы интегрирования.............................................. 6 Задачи и упражнения........................................................................ 14 Лекция 2. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ (продолжение) ........................ 15 1. Интегрирование выражений, содержащих квадратный трехчлен 15 2. Интегрирование простейших рациональных дробей................ 17 3. Интегрирование простейших иррациональных функций........... 18 4. Интегрирование тригонометрических функций......................... 20 Задачи и упражнения........................................................................ 23 Литература...................................................................................... 24 Ответы к задачам и упражнениям................................................. 25
Учебное издание МЕТЕЛЬСКИЙ Василий Михайлович ВЫСШАЯ МАТЕМАТИКА
Неопределенный интеграл
Учебно-методическое пособие
Ответственный за выпуск И. В. Лаврик
Компьютерный набор В. М. Метельский Компьютерная верстка С. Л. Дудко Корректор Н. А. Бебель
Подписано в печать 13.08.2007 г. Формат 60х841/16. Бумага газетная. Гарнитура «Times New Roman». Отпечатано способом ризографии в авторской редакции. Усл. печ. л. 1,62. Уч.-изд. л. 1,4. Тираж 250 экз. Заказ 89.
Издатель и полиграфическое исполнение: Учреждение образования «Частный институт управления и предпринимательства». 220086, г. Минск, ул. Славинского 1, корп. 3.
|

 ; б)
; б) 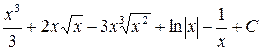 ;
;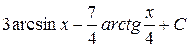 ; г)
; г) 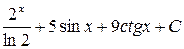 ;
;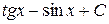 ; е)
; е) 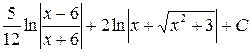 ;
;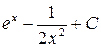 ; з)
; з) 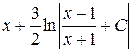 .
.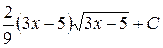 ; б)
; б)  ;
; ; г)
; г) 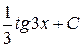 ;
;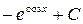 ; е)
; е) 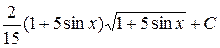 ;
;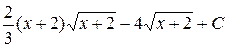 ; з)
; з) 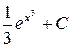 ;
; ; к)
; к) 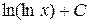 ;
;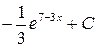 ; м)
; м) 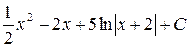 .
.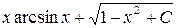 ; б)
; б) 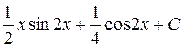 ;
;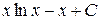 ; г)
; г) 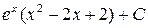 ;
;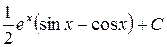 ; е)
; е)  ;
;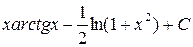 ; з)
; з)  ;
;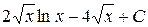 .
. ; б)
; б) 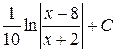 ;
; ; г)
; г) 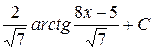 ;
;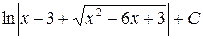 ; е)
; е) 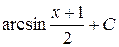 ;
;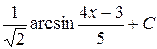 ; з)
; з) 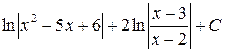 ;
; ;
;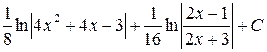 ;
;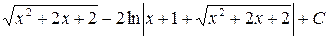 ;
; .
.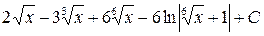 ; б)
; б) 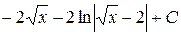 ;
;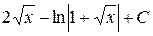 ; г)
; г)  ;
;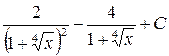 ; е)
; е)  .
.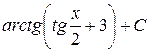 ; б)
; б) 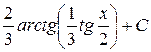 ;
; ; г)
; г) 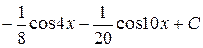 ;
;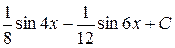 ; е)
; е)  ;
;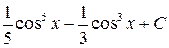 ; з)
; з) 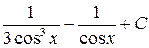 ;
;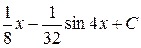 ; к)
; к) 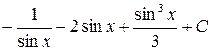 ;
;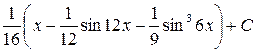 .
. Лицензия ЛИ № 02330/0133342 от 29.06.2004 г.
Лицензия ЛИ № 02330/0133342 от 29.06.2004 г.


