Производная. Первообразная. Неопределенный интеграл. Интегрирование. Подынтегральная функция. Подынтегральное выражение. Переменная интегрирования. Интегральная кривая. Непосредственное интегрирование. Интегрирование заменой переменной. Интегрирование по частям.
Понятие первообразной функции. Неопределенный интеграл
Одной из основных задач дифференциального исчисления является отыскание производной заданной функции. В интегральном исчислении решается обратная задача: по данной функции 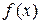 найти функцию
найти функцию  , производная которой была бы равна функции
, производная которой была бы равна функции 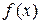 , т.е.
, т.е.  . Искомую функцию
. Искомую функцию  называют первообразной для функции
называют первообразной для функции 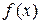 .
.
Определение 1. Функция  называется первообразной для функции
называется первообразной для функции 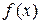 на интервале
на интервале  , если она дифференцируема на
, если она дифференцируема на  и для любого
и для любого  выполняется равенство
выполняется равенство
.
Например, функция  является первообразной для функции
является первообразной для функции  на всей числовой прямой, так как при любом значении
на всей числовой прямой, так как при любом значении  , т.е. выполняется равенство
, т.е. выполняется равенство  ; функция
; функция  является первообразной для функции
является первообразной для функции  на всей числовой прямой, так как в каждой точке
на всей числовой прямой, так как в каждой точке  .
.
Задача отыскания по данной функции 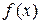 ее первообразной
ее первообразной  решается неоднозначно. Действительно, если
решается неоднозначно. Действительно, если  является первообразной для функции
является первообразной для функции  , т.е.
, т.е.  , то функция
, то функция  , где C – произвольная постоянная, также является первообразной для
, где C – произвольная постоянная, также является первообразной для  , так как
, так как  . Например, для функции
. Например, для функции  первообразной является не только функция
первообразной является не только функция  , но и функция
, но и функция  , так как
, так как  . Таким образом, справедлива следующая теорема:
. Таким образом, справедлива следующая теорема:
Теорема 1. Если функция  является первообразной для функции
является первообразной для функции 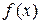 на интервале
на интервале  , то множество всех первообразных для
, то множество всех первообразных для 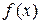 задается формулой
задается формулой  , где C – произвольная постоянная.
, где C – произвольная постоянная.
Определение 2. Множество всех первообразных функций  для функции
для функции  на интервале
на интервале  называется неопределенным интегралом от функции
называется неопределенным интегралом от функции  на этом интервале и обозначается символом
на этом интервале и обозначается символом  , где
, где  – знак интеграла;
– знак интеграла; 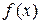 – подынтегральная функция;
– подынтегральная функция;  – подынтегральное выражение;
– подынтегральное выражение;  – переменная интегрирования.
– переменная интегрирования.
Таким образом:
 ,
,
где  – некоторая первообразная для
– некоторая первообразная для 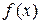 на интервале
на интервале  ; C – произвольная постоянная.
; C – произвольная постоянная.
Например, поскольку функция  является первообразной для функции
является первообразной для функции  , то
, то  .
.
Операция нахождения неопределенного интеграла от данной функции называется интегрированием этой функции. Интегрирование представляет собой операцию, обратную дифференцированию. Для того чтобы проверить, правильно ли выполнено интегрирование, достаточно продифференцировать результат и получить при этом подынтегральную функцию.
Пример 1. Проверить, что  .
.
Решение. Продифференцируем результат интегрирования:
 . Получили подынтегральную функцию, следовательно, интегрирование выполнено верно.
. Получили подынтегральную функцию, следовательно, интегрирование выполнено верно.
Геометрически неопределенный интеграл представляет собой семейство плоских кривых  , смещенных относительно друг друга вдоль оси
, смещенных относительно друг друга вдоль оси  . График каждой первообразной (кривой) называется интегральной кривой.
. График каждой первообразной (кривой) называется интегральной кривой.

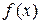 найти функцию
найти функцию  , производная которой была бы равна функции
, производная которой была бы равна функции  . Искомую функцию
. Искомую функцию  , если она дифференцируема на
, если она дифференцируема на  выполняется равенство
выполняется равенство является первообразной для функции
является первообразной для функции  на всей числовой прямой, так как при любом значении
на всей числовой прямой, так как при любом значении  , т.е. выполняется равенство
, т.е. выполняется равенство  является первообразной для функции
является первообразной для функции  на всей числовой прямой, так как в каждой точке
на всей числовой прямой, так как в каждой точке  .
. , т.е.
, т.е.  , где C – произвольная постоянная, также является первообразной для
, где C – произвольная постоянная, также является первообразной для  . Например, для функции
. Например, для функции  , но и функция
, но и функция  , так как
, так как  . Таким образом, справедлива следующая теорема:
. Таким образом, справедлива следующая теорема: , где
, где  – знак интеграла;
– знак интеграла;  – подынтегральное выражение;
– подынтегральное выражение;  – переменная интегрирования.
– переменная интегрирования. ,
, является первообразной для функции
является первообразной для функции  , то
, то  .
. .
. . Получили подынтегральную функцию, следовательно, интегрирование выполнено верно.
. Получили подынтегральную функцию, следовательно, интегрирование выполнено верно. , смещенных относительно друг друга вдоль оси
, смещенных относительно друг друга вдоль оси  . График каждой первообразной (кривой) называется интегральной кривой.
. График каждой первообразной (кривой) называется интегральной кривой.


