Интегрирование тригонометрических функций. 1.Интегралы вида , где R – рациональная функция от и , приводятся к интегралам от рациональны
1. Интегралы вида Действительно,
где
Пример 7. Вычислить интеграл Решение. Положим
2. Интегралы вида
Пример 8. Найти интеграл Решение. Так как
3. Интегралы вида
Если одно из чисел
Пример 9. Найти интеграл Решение.
Пример 10. Найти интеграл Решение.
ЗАДАЧИ И УПРАЖНЕНИЯ
1. Найти интегралы:
a) г) ж) к)
2. Найти интегралы:
а) г)
3. Найти интегралы:
а) г) ж) к)
ЛИТЕРАТУРА 1. Ильин В. А., Позняк Э. Г. Основы математического анализа. Ч. I. – М.: Наука, 1982. – 616 с.
2. Гусак А. А. Математический анализ и дифференциальные уравне-ния.– Мн.: ТетраСистемс, 1998. – 416 с.
3. Гусак А. А. Высшая математика: Учеб. пособие для студентов вузов: В 2 т. – Мн., 1998. – 544 с. (1 т.), 448 с. (2 т.).
4. Кремер Н. Ш., Путко Б. А., Тришин И. М., Фридман М. Н. Высшая математика для экономистов: Учебник для вузов / Под ред. проф. Н. Ш. Кремера.– М.: ЮНИТИ, 2002. – 471 с.
5. Яблонский А. И., Кузнецов А. В., Шилкина Е. И. и др. Высшая математика. Общий курс: Учебник / Под общ. ред. С. А. Самаля.– Мн.: Выш. шк., 2000. – 351 с.
ОТВЕТЫ К ЗАДАЧАМ И УПРАЖНЕНИЯМ
|

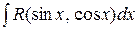 , где R – рациональная функция от
, где R – рациональная функция от  и
и  , приводятся к интегралам от рациональных функций с помощью подстановки
, приводятся к интегралам от рациональных функций с помощью подстановки  (универсальная тригонометрическая подстановка).
(универсальная тригонометрическая подстановка). ,
, 
 ,
,  ,
,  . Тогда
. Тогда ,
, – рациональная функция от переменной
– рациональная функция от переменной  .
.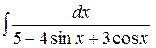 .
. . Тогда
. Тогда 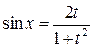 ,
,  ,
, 

 [переходя к переменной x ] =
[переходя к переменной x ] =  .
.
 находятся с помощью тригонометрических формул:
находятся с помощью тригонометрических формул:

 .
. .
.
 , то
, то
 .
. , где
, где  и
и  – четные числа, находятся с помощью формул:
– четные числа, находятся с помощью формул: ;
;  .
. , если
, если  , если
, если  .
.


 .
. .
. [так как
[так как  ] = =
] = =  [замена
[замена  ] = =
] = = 
 .
. ; б)
; б)  ; в)
; в)  ;
; ; д)
; д)  ; е)
; е)  ;
; ; з)
; з)  ; и)
; и)  ;
; ; л)
; л)  ; м)
; м)  .
. ; б)
; б)  ; в)
; в)  ;
; ; д)
; д)  ; е)
; е)  .
. ; б)
; б) 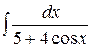 ; в)
; в)  ;
; ; д)
; д)  е)
е) 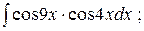
 з)
з)  ; и)
; и) 
 ; л)
; л)  .
.


