Основные свойства неопределенного интеграла
Из определения неопределенного интеграла непосредственно вытекают следующие его свойства: 1. Производная от неопределенного интеграла равна подынтегральной функции; дифференциал от неопределенного интеграла равен подынтегральному выражению:
2. Неопределенный интеграл от дифференциала некоторой функции равен сумме этой функции и произвольной постоянной:
3. Постоянный множитель можно выносить за знак неопределенного интеграла:
4. Неопределенный интеграл от алгебраической суммы непрерывных функций равен алгебраической сумме неопределенных интегралов:
Заметим, что свойство 4 справедливо для любого конечного числа слагаемых. 5. Если
Таблица основных неопределенных интегралов
Данную таблицу можно получить, пользуясь тем, что интегрирование есть операция, противоположная дифференцированию. Часть формул этой таблицы непосредственно следует из таблицы производных основных элементарных функций. Справедливость остальных формул легко проверяется дифференцированием. 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16.
В данной таблице переменная интегрирования х может быть как независимой переменной, так и функцией от независимой переменной (см. свойство 5). Например, если в формуле 7 вместо переменной х взять функцию
Интегралы, содержащиеся в этой таблице, называются табличными. Их необходимо знать наизусть, так как более сложные интегралы сводятся к табличным путем преобразований подынтегральной функции.
4. Основные методы интегрирования
А. Непосредственное интегрирование. Этот метод заключается в непосредственном применении таблицы неопределенных интегралов и свойств 1 - 5 неопределенного интеграла. Иногда требуется предварительное преобразование подынтегральной функции. При непосредственном вычислении неопределенных интегралов часто используются следующие преобразования дифференциала (операция «под-несения под знак дифференциала»):
В общем случае:
Пример 2. Найти интеграл Решение. Воспользуемся свойствами 3 и 4 неопределенного интеграла:
Находим каждый из полученных табличных интегралов, используя соответственно формулы 3, 4, 5, 7, 2, 12:
В результате имеем:
Обозначив
Правильность полученного результата проверим дифференцированием:
Пример 3. Найти интеграл
Решение. Для нахождения данного интеграла воспользуемся свойством 5 неопределенного интеграла. Так как
Пример 4. Найти интеграл
Решение. Преобразуем подынтегральную функцию:
=
Пример 5. Найти интеграл
Решение. Интеграл не табличный, поэтому преобразуем его, воспользовавшись основным тригонометрическим тождеством
B. Метод замены переменной (подстановки). Непосредственно вычислить интегралы с помощью таблицы неопределенных интегралов и свойств 1 - 5 удается довольно редко. Поэтому для вычисления неопределенных интегралов используют другие методы, среди которых одним из важнейших является метод замены переменной (или метод подстановки). Суть этого метода заключается во введении новой переменной интегрирования. При этом исходный интеграл сводится к новому интегралу, который либо является табличным, либо легко к нему сводится путем преобразований подынтегральной функции. Пусть требуется вычислить интеграл
Формула (1) называется формулой замены переменной в неопределенном интеграле. После вычисления интеграла в правой части этого равенства следует перейти от новой переменной интегрирования Формулу (1) можно применять и в обратном порядке, т.е. справа налево. В этом случае используют подстановку
Пример 6. Найти интеграл Решение. Сделаем замену Заметим, что данный интеграл можно было вычислить непосредственно, воспользовавшись следующим преобразованием дифференциала:
Пример 7. Найти интеграл Решение. Полагаем
Пример 8. Найти интеграл Решение. Положим
Пример 9. Найти интеграл Решение. Пусть
При вычислении интегралов необходимо помнить следующее правило: если числитель подынтегральной функции f(x) равен производной знаменателя, то справедлива формула
или
Пример 10. Найти интеграл Решение. Так как В заключение заметим, что общих методов выбора подстановки не существует. Умение правильно определить подстановку приобретается практикой и базируется на твердых знаниях табличных интегралов и хорошем владении техникой дифференцирования.
С. Метод интегрирования по частям. Пусть
или
Интегрируя обе части последнего равенства и учитывая, что
Формула (4) называется формулой интегрирования по частям. Метод интегрирования по частям состоит в том, что подынтегральное выражение представляется в виде произведения двух сомножителей В некоторых случаях для нахождения искомого интеграла формулу интегрирования по частям приходится применять несколько раз. Большая часть интегралов, берущихся по формуле (4), может быть разбита на три группы: 1. К первой группе относятся интегралы вида
где 2. Ко второй группе относятся интегралы вида
где 3. К третьей группе относятся интегралы вида
где
Пример 11. Найти интеграл Решение. Данный интеграл относится к первой группе, поэтому полагаем
= [интеграл
Пример 12. Найти интеграл Решение. Положим
Интеграл в правой части полученного равенства не является табличным, но он значительно проще исходного, так как степень переменной
Пример 13. Найти интеграл Решение. Пусть
Перенося интеграл из правой части полученного равенства в левую, получаем
Следовательно,
|

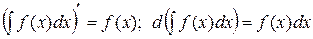 .
. .
. (c – const,
(c – const,  ).
). .
. , а
, а 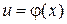 – произвольная функция, имеющая непрерывную производную, то
– произвольная функция, имеющая непрерывную производную, то  .
. .
.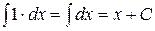 .
.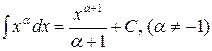 .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. , то получим:
, то получим: .
. ,
, ,
, ,
, ,
,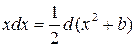 ,
, ,
, ,
, .
. .
. .
.
 .
. ;
; 
 ;
;  ;
; ;
;  .
.
 .
. , окончательно получим
, окончательно получим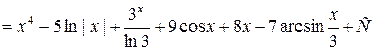 .
.

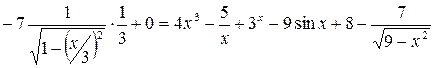 . Получили подын-тегральную функцию. Значит, интеграл найден правильно.
. Получили подын-тегральную функцию. Значит, интеграл найден правильно. .
. , то
, то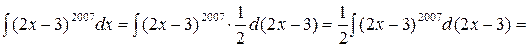
 .
. .
.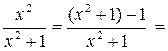 [делим почленно числитель на знаменатель] =
[делим почленно числитель на знаменатель] = . Тогда исходный интеграл примет вид
. Тогда исходный интеграл примет вид .
. .
. . Получим
. Получим
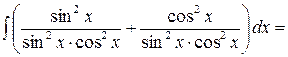

 .
. , который не вычисляется непосредственно. Сделаем замену переменной
, который не вычисляется непосредственно. Сделаем замену переменной 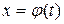 , где
, где  – дифференцируемая функция. Тогда
– дифференцируемая функция. Тогда  и исходный интеграл приобретет вид
и исходный интеграл приобретет вид . (1)
. (1) к старой переменной
к старой переменной  .
. , тогда
, тогда  =
=  .
.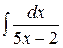 .
. , тогда
, тогда  , а
, а  . Найдем
. Найдем 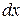 :
:  . Следовательно,
. Следовательно, 
 =
=  . Возвращаясь к переменной
. Возвращаясь к переменной  .
. . (Сделать самостоятельно).
. (Сделать самостоятельно). .
. . Отсюда находим
. Отсюда находим 
 . Следовательно:
. Следовательно: .
. .
. , тогда
, тогда 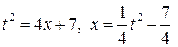 ,
,  ,
, 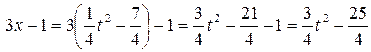 . Таким образом:
. Таким образом:
 .
. .
. , тогда
, тогда  . Из последнего равенства выразим произведение
. Из последнего равенства выразим произведение  , входящее в подынтегральное выражение:
, входящее в подынтегральное выражение:  . Следовательно:
. Следовательно: .
. , (2)
, (2) . (3)
. (3) .
. , то исходный интеграл можно записать
, то исходный интеграл можно записать  . Замечая, что
. Замечая, что  , по формуле (2) получим
, по формуле (2) получим  .
. и
и  – две дифференцируемые функции. По свойству дифференциала
– две дифференцируемые функции. По свойству дифференциала ,
, .
. , получаем
, получаем . (4)
. (4) и
и  ; в качестве u обычно выбирается функция, которая при дифференцировании упрощается, в качестве dv – оставшаяся часть подынтегрального выражения, содержащая dx, из которой путем интегрирования можно определить функцию
; в качестве u обычно выбирается функция, которая при дифференцировании упрощается, в качестве dv – оставшаяся часть подынтегрального выражения, содержащая dx, из которой путем интегрирования можно определить функцию  . Затем, после нахождения
. Затем, после нахождения  и
и  ,
,  ,
,  ,
,  ,
,  ,
, 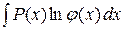 ,
, – многочлен. Для их вычисления следует применить формулу (4), полагая в ней
– многочлен. Для их вычисления следует применить формулу (4), полагая в ней  .
. ,
,  ,
,  ,
, – некоторое число. Для их вычисления следует положить
– некоторое число. Для их вычисления следует положить  , а
, а  ,
,  ,
,  соответственно.
соответственно. ,
,  ,
,  ,
,  ,
, и
и 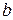 – некоторые числа. Эти интегралы вычисляются двукратным интегрированием по частям, причем за
– некоторые числа. Эти интегралы вычисляются двукратным интегрированием по частям, причем за  .
. ,
,  . Тогда
. Тогда  ,
, 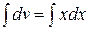 ,
,  (при нахождении
(при нахождении  можно положить равной нулю). Применяя формулу (4), получаем
можно положить равной нулю). Применяя формулу (4), получаем =
= был вычислен ранее (см. пример 4)] =
был вычислен ранее (см. пример 4)] =
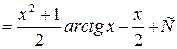 , где
, где  .
. .
. . Тогда
. Тогда  ,
,  . По формуле (4) получаем
. По формуле (4) получаем .
. того же типа, что и в исходном интеграле. Для вычисления интеграла
того же типа, что и в исходном интеграле. Для вычисления интеграла  еще раз применим формулу (4), полагая на этот раз
еще раз применим формулу (4), полагая на этот раз  . Получим
. Получим 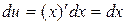 ,
, 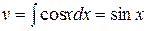 . Следовательно:
. Следовательно: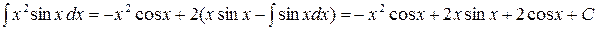 .
. .
. . Тогда
. Тогда  ,
,  =
= 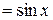 . Применяя формулу интегрирования по частям, получим
. Применяя формулу интегрирования по частям, получим  . Последний интеграл снова вычисляем интегрированием по частям, положив
. Последний интеграл снова вычисляем интегрированием по частям, положив  , откуда найдем
, откуда найдем  . Тогда
. Тогда .
. .
. .
.


