Основные теоретические сведения. Электромагнитными волнами называются возмущения электромагнитного поля, распространяющиеся в пространстве
Электромагнитными волнами называются возмущения электромагнитного поля, распространяющиеся в пространстве. Исследуем процесс распространения волн. Рассмотрим двухпроводную линию, неограниченно простирающуюся в обе стороны, и примем, что источник переменного тока создает в какой-либо точке 0 линии (рис. 5.1 а) электрическое поле Один из способов передачи электрического поля заключается в возникновении токов проводимости. При этом электроны в проводах перемещаются вдоль линии и при движении переносят свой электрический заряд, а вместе с ним и электрическое поле. Существует другой процесс передачи поля, который в очень многих явлениях играет главную роль. Он был открыт Максвеллом и состоит в распространении электромагнитных волн. Предположим, что в данный момент времени электрическое поле Но согласно второму основному положению теории Максвелла, изменяющееся магнитное поле вызывает появление вихревого электрического поля. Поэтому в последующий момент времени возникнет электрическое поле Если бы проводов линии не было, то линии поля
Возрастающее электрическое поле В последующие моменты времени явления будут происходить аналогично. Возрастающее поле Отметим, что выше мы рассматривали только половину линии, находящуюся справа от точки 0. Очевидно, что такие же явления будут происходить и в левой части линии, и поэтому поля будут распространяться в обе стороны от места первоначального возмущения. Таким образом, существуют два различных процесса передачи поля: с помощью токов проводимости и при помощи токов смещения (электромагнитных волн). Допустим, что в точке x = 0 (рис. 5.2) безграничной линии электрическое поле изменяется по гармоническому закону
Электромагнитное поле будет распространяться вдоль линии, и, следовательно, в какой-либо точке линии, удаленной на расстояние х от точки x = 0, также возникнут гармонические колебания поля. Однако распространение поля происходит с конечной скоростью v, так что колебания в точке х будут запаздывать относительно колебаний в x = 0 на время распространения импульса t = x/v. Следовательно, колебания электрического поля в точке х запишутся в виде
Поскольку максимумы электрического поля при распространении электромагнитного импульса совпадают с максимумами магнитного поля. Поэтому колебания магнитного поля в точке x = 0 будут H = H 0 sin wt, а в точке х
Формулы (5.2) и (5.3) выражают закон изменения электрического и магнитного полей в волне, распространяющейся в одном определенном направлении, а именно в направлении положительной оси X. Они называются уравнением волны. Если волна распространяется в противоположном направлении (вдоль отрицательной оси X), уравнение волны будет
Мгновенное распределение электрических и магнитных полей в электромагнитной волне изображено на рис. 5.2. Для данного момента времени электрическое и магнитное поля достигают максимума в одних и тех же точках и в одних и тех же точках проходят через нуль. Если же следить за изменениями полей в какой-либо определенной точке линии, то оба поля Расстояние между двумя точками, в которых колебания отличаются по фазе на 2p (например, между двумя соседними максимумами (рис. 5.2) есть длина электромагнитной волны l. Она равна расстоянию, на которое распространяется волна за время одного колебания – периода Т. Если v – скорость распространения электромагнитных волн, то
Пользуясь соотношением (5.5) и учитывая, что w = 2 p / Т, уравнения волны можно записать и в следующем виде:
где k = 2 p / l – волновое число. Такая же формула справедлива и для магнитного поля
Перечислим свойства электромагнитных волн. Электромагнитные волны – поперечные волны: векторы Векторы Модули векторов
которое справедливо для любой бегущей электромагнитной волны. В (5.8) e 0 = 8.85×10–12 Ф/м – электрическая постоянная, m 0 = 12.566×10–7 Гн/м – магнитная постоянная, e – диэлектрическая проницаемость среды, m – магнитная проницаемость среды. Из выражения (5.8) следует, что вектора меняются в одной и той же точке среды синфазно. Переменное электромагнитное поле распространяется в пространстве в виде волн, фазовая скорость которых равна
где Скорость распространения электромагнитных волн вдоль проводов длинной линии связана с электрическими и магнитными характеристиками линии следующим образом:
где
Подставив (5.11) в (5.10) легко убедиться, что скорость распространения волн вдоль длинной линии определяется формулой (5.9). Точно такой же результат получается при использовании проводов любой формы и при любом их взаимном расположении: скорость электромагнитных волн, распространяющихся вдоль линии проводов не зависит от характеристик линии. При подключении длинной линии к источнику постоянного напряжения U в линии при распространении электромагнитной волны возникнет ток силы
где Если концы линии замкнуты на активное сопротивление R, равное волновому сопротивлению Распространение импульса электромагнитной волны вдоль длинной линии можно изучать в двух режимах: холостого хода и короткого замыкания. Если линия на конце разомкнута (режим холостого хода), то в месте разрыва линии сила тока, возникающего при распространении сигнала, равна нулю, и таким образом после достижения волной конца разомкнутой линии вдоль линии начнёт распространяться с той же скоростью отражённый сигнал той же полярности. Если же линия на конце замкнута (режим короткого замыкания), то при достижении волной конца линии возникает противофазная обратная волна тока, и, следовательно, по линии распространяется импульс обратной полярности.
|

 . Опыт показывает, что электрическое поле распространяется вдоль линии. Опишем процессы, с помощью которых происходит распространение поля.
. Опыт показывает, что электрическое поле распространяется вдоль линии. Опишем процессы, с помощью которых происходит распространение поля. . Так как поле
. Так как поле  и направление тока смещения
и направление тока смещения  совпадает с направлением
совпадает с направлением  направлено так, как показано на рис. 5.1а.
направлено так, как показано на рис. 5.1а. . Оно будет направлено так же, как и индукционный ток, который возник бы в замкнутом проводнике под действием возрастающего поля
. Оно будет направлено так же, как и индукционный ток, который возник бы в замкнутом проводнике под действием возрастающего поля  а)
а)
 б)
б)
 в)
в)
 . Из рис. 5.1 а видно, что поле
. Из рис. 5.1 а видно, что поле  , а это последнее, увеличиваясь, приведет к возникновению магнитного поля
, а это последнее, увеличиваясь, приведет к возникновению магнитного поля  . Поля
. Поля  . (5.1)
. (5.1) . (5.2)
. (5.2) . (5.3)
. (5.3)
 ,
, . (5.4)
. (5.4) . (5.5)
. (5.5) , (5.6)
, (5.6) . (5.7)
. (5.7) в каждой рассматриваемой точке поля.
в каждой рассматриваемой точке поля.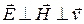 .
. , (5.8)
, (5.8) , (5.9)
, (5.9) м/с – скорость электромагнитных волн в вакууме.
м/с – скорость электромагнитных волн в вакууме. , (5.10)
, (5.10)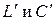 – индуктивность и ёмкость, приходящиеся на единицу длины линии. Однако зависимости этих величин от геометрических параметров линии таковы, что их произведение определяется и зависит только от электрических и магнитных свойств среды, в которую помещена линия. Например, для коаксиального кабеля зависимости индуктивности и ёмкости от радиусов
– индуктивность и ёмкость, приходящиеся на единицу длины линии. Однако зависимости этих величин от геометрических параметров линии таковы, что их произведение определяется и зависит только от электрических и магнитных свойств среды, в которую помещена линия. Например, для коаксиального кабеля зависимости индуктивности и ёмкости от радиусов  и
и  центрального провода и внешней оболочки имеют вид:
центрального провода и внешней оболочки имеют вид: ,
, 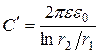 . (5.11)
. (5.11) , (5.12)
, (5.12) – волновое сопротивление линии.
– волновое сопротивление линии.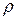 , то при достижении электромагнитной волной конца линии сила тока в активном сопротивлении R будет равна силе тока при распространении электромагнитного поля вдоль линии. Поэтому никакого изменения силы тока в линии после достижения её конца не происходит. В цепи всё время течёт одинаковый постоянный ток I c момента замыкания цепи.
, то при достижении электромагнитной волной конца линии сила тока в активном сопротивлении R будет равна силе тока при распространении электромагнитного поля вдоль линии. Поэтому никакого изменения силы тока в линии после достижения её конца не происходит. В цепи всё время течёт одинаковый постоянный ток I c момента замыкания цепи.


