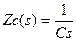E. A and C are both correct
Solution: 1) 2) Answer: E.
95. What is correct inverse Laplace transform VC(t) for the function VC(s)=(- 0.6s/s2+4) A. – 0.6 cos2t B.0.6cos2t C.- 0.6sin2t D.0.6sin2t E.0.6e2t
Solution:
Answer: A.
96. When we transform the circuit from time domain into S-domain the admittance of inductor is A.YL(s)=Ls B. YL(s)=Ls with iL(0)=0 C. YL(s)=1/Ls D. YL(s)=1/Ls with iL(0)=0 E. YL(s)=1/L
Solution: ZL=Ls with iL(0)=0; YL=1/ZL=1/Ls with iL(0)=0; Answer: D. 97. Define impedance of the circuit in the s-domain respectively points A and B (fig.11). A.Z(s)=RCs+1 B.Z(s)=Cs+2R C.Z(s)=RCs+R D.Z(s)= R(RCs+1)/(RCs+2) E. Z(s)=R(RCs+2)/(RCs+1) Fig.11
Solution:
Answer: E.
98. Find the mistake in process of transformation of time-domain circuit in s-domain circuit. A. wrong representation of the capacitor impedance B. wrong representation of the inductor impedance C. wrong representation of the capacitor initial condition current source D. wrong representation of the inductor initial condition current source E. there is no mistake in process of circuit’s conversion
Solution: I(t)=I(s); ZR(s)=R; ZC(s)=1/Cs; IC(s)=CsVC(s) – CVC(0); ZL(s)=Ls; IL(s)=(1/Ls)*VL(s)+ iL(0)/s; Wrong representation of the inductor initial condition current source.
|
Capacitor impedance and voltage source, which is connected with the capacitor in series;
Capacitor admittance and current source, which is connected with the capacitor in parallel.
