Answer: D.
99. The time domain equation is 10i1+0.02(di1/dt)-0.02(di2/dt)=100. What is the view of the equation in the s-domain? A. (10+0.02s)I2(s)-0.02sI1(s)=100/s B. (10+0.02s)I1(s)-0.02sI2(s)=100 C. (10+0.02s)I1(s)-0.02sI2(s)=100/s D. (10+0.04s)I1(s)-0.04sI2(s)=100/s E. 0.02sI1(s)-0.02sI2(s)=100/s
Solution:
t-domain:
10i1+0.02(di1/dt)-0.02(di2/dt)=100 s-domain: 10I1+0.02sI1 – 0.02sI2=100/s (10+0.02s)I1 – 0.02sI2=100/s Answer: C. 100. What must be Zload to have maximum average power transfer conditions fulfillment, if ZT=50+j70? A. 50 - j70 B. 50+j70 C. 70+j50 D. 70 – j50 E. 100+j20 Solution:
if XT = – XL, then denominator is minimized, I is maximized and P is maximized, thus Zload to have maximum average power transfer conditions fulfillment, if ZT=50+j70 has to be 50-j70. Answer: A.
101. What numbers of natural poles are corresponded to sinusoidal type of response? A)2 and 4 B) 1 and 3 C) 1 and 9 D) 1 and 5
Answer: D
102. Define impedance of the circuit in the s-domain respectively points A and B (fig.12).
B).Z(s)=CLs+2R C).Z(s)=RLCs+R D).Z(s)= R(RLCs+1)/(RCs+2) E) Z(s)=R(RLCs+2)/(RCs+1) Fig.12 Solution: ZR(s)=R ZC(s)=1/Cs ZL(s)=Ls Zeq(s)=(R/Cs)/(R+1/Cs)+Ls=(RLCs2+Ls+R)/(RCs+1) Answer:A 103. Find the mistake in process of transformation of time-domain circuit in s-domain circuit.
A) wrong direction of the capacitor initial condition current source B) wrong representation of the inductor impedance C) wrong representation of the capacitor initial condition current source D) wrong representation of the inductor initial condition current source E) there is no mistake in process of circuit’s conversion
|
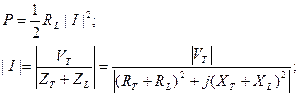
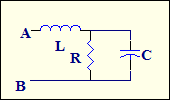A).Z(s)=RLCs2+Ls+R/RCs+1
