Примеры решения аудиторных задач
Определить Решение. Используя известные формулы [10, с.317] для точечных оценок математического ожидания и дисперсии нормально распределенных величин, получим Нижнюю границу вычислим по формуле:
Здесь Для оценки верхней границы воспользуемся выражением:
Значит, можно с вероятностью не менее 0,9 утверждать, что среднее квадратичное отклонение времени безотказной работы испытываемых изделий не превысит 77,4 ч, а наработка на отказ будет не менее 109,6 ч.
Определить двусторонний доверительный интервал для интенсивности отказов при Решение. Для вычисления
Нижняя граница интенсивности отказов
Верхняя граница интенсивности отказов
Из решения задачи следует, что с вероятностью, не меньшей 0,9, можно считать, что интервал интенсивностей 6.4 Задачи для самостоятельного решения
Задача 2. Определить доверительный интервал для Т 0 при доверительной вероятности 0,9, если результаты испытаний по плану NRT следующие: N=2; T=72 ч; tp=140 ч; число отказов n=4. Задача 3. Определить двухсторонний доверительный интервал для КГ при доверительной вероятности ^ 0,9 при условии, что T0= 100 ч, T= 1 ч, число восстановлений 10.
Контрольные вопросы и задания
2.Какие существуют планы испытаний? 3. Что даст замена плана 4. Какие можно предложить планы для сокращения времени испытания? 5. Как скажется уменьшение выборки на достоверности и точности испытаний? 6. Как изменится достоверность испытаний, если при тех же требованиях к точности увеличить объем выборки? 7. Чем вызвана необходимость в интервальных оценках ПН вместо точечных? 8. Что такое уровень значимости? 9. Назовите особенности статистической обработки ограниченного объема полученного ряда времен работы до отказа. 10. Чем необходимо руководствоваться при выдвижении гипотезы о справедливости того или иного закона распределения?
|

 ;
; 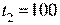 ;
;  ;
;  ;
;  ;
; 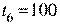 ;
; 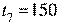 ;
;  ;
;  ;
;  .
. и
и  , а также нижнюю
, а также нижнюю  и верхнюю
и верхнюю  границы с доверительной вероятностью
границы с доверительной вероятностью  .
. ;
;  .
.
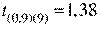


 10 изделий, время безотказной работы которых распределено по экспоненциальному закону, получены следующие значения наработок в часах
10 изделий, время безотказной работы которых распределено по экспоненциальному закону, получены следующие значения наработок в часах  ;
;  ;
;  ;
;  ;
;  ;
;  ;
;  ;
;  ;
; 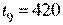 ;
; 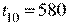 .
. .
. и
и  найдем:
найдем: ;
;  ;
;  ;
; ;
;  .
.

 накрывает параметр
накрывает параметр  .
. на
на  ,
,  ,
,  на
на  ?
?


