Основний закон радіоактивного розпаду, період напіврозпаду, активність
Розрізняють два види радіоактивності – природну і штучну. Досі ми розглядали природну радіоактивність – перетворення нестійких ізотопів одного елемента в ізотопи інших елементів при a - і b -розпадах або випромінювання ядрами g -квантів, які відбуваються в природних умовах самодовільно, тобто без зовнішніх втручань. Штучна радіоактивність – розпад штучно отриманих ізотопів хімічних елементів внаслідок різних ядерних реакцій. Штучна радіоактивність була відкрита в 1934 р. подружжям Ірен і Фредеріком Жоліо-Кюрі. Обидва види радіоактивності – природна і штучна – підпорядковуються одним і тим же законам. Основний закон радіоактивного розпаду. Отримаємо закон радіоактивного розпаду в двох формах – диференціальній та інтегральній. Внаслідок самодовільності радіоактивного розпаду число ядер dN, які розпадаються за проміжок часу від t до – dN = l N dt. (10.8) Знак “–” в (10.8) перед dN характеризує зменшення числа вихідних радіоактивних ядер за проміжок часу dt. Стала величина l називається постійною радіоактивного розпаду. Вона не залежить від зовнішніх умов і визначається лише внутрішніми властивостями атомного ядра хімічного елемента. Співвідношення (10.8) визначає по суті закон радіоактивного розпаду в диференціальній формі, який формулюється наступним чином: відносне зменшення кількості радіоактивних ядер за одиницю часу, тобто –dN/Ndt, є величина стала, яка називається постійною радіоактивного розпаду l. Або іншими словами: за одиницю часу розпадається одна і та ж сама частка наявних радіоактивних ядер. Для отримання закону радіоактивного розпаду в інтегральній формі розділимо змінні в рівнянні (10.8)
та проінтегруємо це диференційне рівняння з поділеними змінними (див. розділ 1 в першому томі) В результаті отримуємо ln N = – l t + C, (10.9) де С – постійна інтегрування, значення якої можна знайти з початкових умов. Будемо вважати, що у вихідний момент часу t = 0 початкова кількість радіоактивних ядер становила N 0. Тоді з рівняння (10.9) маємо, що постійна інтегрування С = ln N 0. Підставляючи це значення постійної інтегрування в (10.9), отримуємо ln N – ln N0 = –lt. (10.10) Далі скористаємося очевидними співвідношеннями: ln N – ln N 0 = В результаті рівняння (10.10) набуває вигляд
Оскільки логарифми є рівними, то повинні бути рівними і вирази, що стоять під знаком логарифмів. Звідси отримуємо закон радіоактивного розпаду в інтегральній формі: N = N 0 е–lt. (10.11)
Період напіврозпаду. Для оцінки стійкості радіоактивних ядер відносно їх розпаду вводять поняття періоду напіврозпаду T 1/2. Період напіврозпаду T 1/2 визначається як той час, протягом якого розпадається половина вихідної кількості, тобто N 0/2, радіоактивних ядер речовини. Відповідно за два періоди напіврозпаду залишається четверта частина радіоактивних ядер, що не розпалися (мал. 10.7). Знайдемо зв’язок періоду напіврозпаду T 1/2 з постійною радіоактивного розпаду l. Оскільки в момент часу t = T 1/2 кількість радіоактивних ядер N = N 0/2, то з рівняння (10.11) маємо Т 1/2 = Отриманий зв’язок між Т 1/2 і l показує, що чим більша постійна радіоактивного розпаду, тим меншим є період напіврозпаду. У радіоактивних елементів періоди напіврозпаду Т 1/2 змінюються в дуже широких межах. Наприклад, для ізотопу урану При дослідженні проходження ізотопів Умовно прийнято вважати, що радіонукліди (ізотопи радіоактивних елементів) практично перестають діяти через час, що становить 10 періодів напіврозпаду. Згідно з законом радіоактивного розпаду
через час t = 10 T 1/2 кількість радіоактивних ядер буде рівною
тобто зменшиться майже в тисячу разів. Звідси випливає, що оскільки період напіврозпаду ізотопів Активність.Активністю А називають швидкість радіоактивного розпаду, тобто кількість розпадів за одиницю часу. Оскільки енергія виділяється при кожному акті розпаду, то загальна кількість енергії, що виділяється внаслідок радіоактивного розпаду за одиницю часу, буде визначатися саме активністю. Формула для активності А має такий вигляд: А = де були враховані закон радіоактивного розпаду (10.11) та зв’язок між періодом напіврозпаду T 1/2 і постійною радіоактивного розпаду l, що дається виразом (10.12). З формули (10.13) випливає важливий висновок: активність А радіоактивного ізотопу (радіонукліду) тим більша, чим більша кількість радіоактивних ядер N в даний момент часу і чим менший період напіврозпаду T 1/2. Тому при однаковому значенні N активність А, а з нею і небезпека радіоактивного ураження, буде визначатися радіонуклідами з малим періодом напіврозпаду. Таким найбільш небезпечним радіонуклідом в перші 3 місяці після Чорнобильської аварії був радіоактивний йод З формули (10.13) видно також, що з плином часу активність А зменшується тому, що зменшується кількість радіоактивних ядер. Дійсно, оскільки N = N 0 e–lt, то А = lN0e–lt = А0 e–lt , (10.14) де А 0 = lN 0 – вихідне значення активності радіонукліда в момент часу t = 0. Цей результат означає, що зменшення активності з часом описується законом радіоактивного розпаду. Активність вимірюється в таких одиницях: беккерель (Бк) і кюрі (Кі). Беккерель – це активність такого радіонукліду, для якого за одну секунду відбувається один радіоактивний розпад, тобто 1 Бк = 1 розпад/с. Кюрі (Кі) – це суттєво більша одиниця активності: 1 Кі = 3.7×1010 розпадів/ с = 3.7×1010 Бк. Застосовуються дрібні одиниці – мілікюрі (мКі), мікрокюрі (мкКі), нанокюрі (нКі) тощо, а також кратні одиниці – кілокюрі (кКі), мегакюрі (Мкі), гігокюрі (Гкі) та інші, які мають такий зв’язок з основними одиницями активності: 1 мКі = 10–3 Кі = 3.7×107 Бк, 1 кКі = 103 Кі = 3.7×1013 Бк, 1 мкКі = 10–6 Кі = 3.7×104 Бк, 1 МКі = 106 Кі = 3.7×1016 Бк, 1 нКі = 10–9 Кі = 37 Бк, 1 ГКі = 109 Кі = 3.7×1019 Бк.
|


 , – lt = ln е–lt.
, – lt = ln е–lt. .
. Графік закону радіоактивного розпаду наведений на мал. 10.7. Чим більша постійна радіоактивного розпаду, тим більш швидко спадає крива залежності N (t), що визначає кількість радіоактивних ядер в момент часу t.
Графік закону радіоактивного розпаду наведений на мал. 10.7. Чим більша постійна радіоактивного розпаду, тим більш швидко спадає крива залежності N (t), що визначає кількість радіоактивних ядер в момент часу t. . Звідси отримуємо
. Звідси отримуємо  , що дає після логарифмування
, що дає після логарифмування =
=  . (10.12)
. (10.12) період напіврозпаду складає Т 1/2 = 4.5×109 років, ізотопу кобальту
період напіврозпаду складає Т 1/2 = 4.5×109 років, ізотопу кобальту  Т 1/2 = 5.3 року, для ізотопу літію
Т 1/2 = 5.3 року, для ізотопу літію  Т 1/2 = 0.9 с, а для ізотопу полонію
Т 1/2 = 0.9 с, а для ізотопу полонію  Т 1/2 = 4×10–6 с. Важливо зазначити, що для радіоактивних ізотопів, які здатні довго затримуватися в організмі людини і тварин, періоди напіврозпаду становлять такі значення: для ізотопу йоду
Т 1/2 = 4×10–6 с. Важливо зазначити, що для радіоактивних ізотопів, які здатні довго затримуватися в організмі людини і тварин, періоди напіврозпаду становлять такі значення: для ізотопу йоду  Т 1/2 = 8 діб, для ізотопів стронцію
Т 1/2 = 8 діб, для ізотопів стронцію  та
та  відповідно Т 1/2 = 51 доба та Т1/2 = 28.6 років, для ізотопу цезію
відповідно Т 1/2 = 51 доба та Т1/2 = 28.6 років, для ізотопу цезію  Т1/2 = 30.2 років.
Т1/2 = 30.2 років. ,
,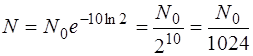 ,
, становить біля 30 років, то населення України буде відчувати вплив цих небезпечних радіонуклідів біля трьох століть після Чорнобильської катастрофи.
становить біля 30 років, то населення України буде відчувати вплив цих небезпечних радіонуклідів біля трьох століть після Чорнобильської катастрофи. , (10.13)
, (10.13) .
.


