Монотонные последовательности. Число e
Определение 1. Последовательность Определение 2. Последовательность Все перечисленные последовательности носят название монотонных. Возрастающие и убывающие последовательности называются также строго монотонными. Рассмотрим некоторые примеры. 1. Последовательность 2. Последовательность 1, 1, 2, 2, …, n, n, … неубывающая и неограниченная. 3. Последовательность Можно показать справедливость следующей теоремы. Теорема 1. Всякая монотонно возрастающая (убывающая) ограниченная сверху (снизу) последовательность имеет предел. Рассмотрим последовательность Используя формулу бинома Ньютона, запишем
Если перейти от Покажем, что эта последовательность ограничена сверху. Опустив в разложении Следовательно,
(так как Но прогрессия
следовательно, Условия теоремы 1 выполнены; отсюда следует существование конечного предела последовательности
|

 называется возрастающей (убывающей), если для любого n
называется возрастающей (убывающей), если для любого n  (
( );
); (
( ).
). ,
, 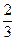 ,
,  , …,
, …,  , … возрастает и ограничена.
, … возрастает и ограничена. ,
,  , …,
, …,  , …убывающая и ограниченная.
, …убывающая и ограниченная.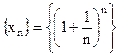 и попытаемся применить к ней эту теорему.
и попытаемся применить к ней эту теорему. в виде
в виде
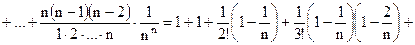
 .
. , то есть увеличить n на единицу, то в предыдущем разложении добавится новый,
, то есть увеличить n на единицу, то в предыдущем разложении добавится новый, 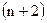 -й положительный член, а каждое из слагаемых в разложении увеличится, так как любой множитель в скобках вида
-й положительный член, а каждое из слагаемых в разложении увеличится, так как любой множитель в скобках вида  заменится большим множителем вида
заменится большим множителем вида  . Отсюда следует, что
. Отсюда следует, что 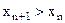 , то есть последовательность монотонно возрастает.
, то есть последовательность монотонно возрастает.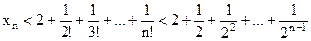
 при
при  ).
). имеет сумму
имеет сумму ,
, .
. играет исключительно важную роль в математике и ее приложениях. Доказывается, что
играет исключительно важную роль в математике и ее приложениях. Доказывается, что  является иррациональным числом.
является иррациональным числом.


