Рассматривая выражения  ,
,  ,
,  , мы предполагали, что последовательности
, мы предполагали, что последовательности  и
и  имеют конечные пределы и
имеют конечные пределы и  .
.
Выясним, каковы будут результаты, когда пределы последовательностей  и
и  (или один из них) бесконечны или когда предел знаменателя (в случае частного) будет равен нулю.
(или один из них) бесконечны или когда предел знаменателя (в случае частного) будет равен нулю.
1. Пусть предел  конечен, а
конечен, а  . Тогда
. Тогда
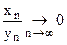 .
.
Действительно,  , так как величина
, так как величина 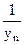 бесконечно малая (обратная бесконечно большой
бесконечно малая (обратная бесконечно большой  ).
).
2. Если  (конечный или бесконечный), а
(конечный или бесконечный), а
 , то
, то  .
.
В самом деле,
 ,
,
так как обратная величина стремится к нулю.
3. Если  , а предел
, а предел  конечен, то
конечен, то  (так как обратное отношение
(так как обратное отношение  ).
).
4. Пусть  . В этом случае предел частного
. В этом случае предел частного  может иметь различные значения или даже вовсе не существовать, это зависит от частного закона изменения переменных. Проиллюстрируем сказанное примерами. Пусть
может иметь различные значения или даже вовсе не существовать, это зависит от частного закона изменения переменных. Проиллюстрируем сказанное примерами. Пусть
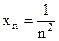 ,
,  ;
;  ,
,  .
.
Тогда 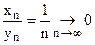 . Если же положить
. Если же положить
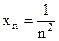 ,
, 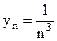 , то
, то  .
.
При  ,
, 
 .
.
Пусть  ,
,  , тогда отношение
, тогда отношение  не имеет предела.
не имеет предела.
Подводя итог рассмотренному, можно утверждать, что знание пределов  и
и  не позволяет судить о пределе их отношения; необходимо знать закон изменения переменных и непосредственно исследовать отношение
не позволяет судить о пределе их отношения; необходимо знать закон изменения переменных и непосредственно исследовать отношение  . Чтобы характеризовать эту особенность, говорят, что выражение
. Чтобы характеризовать эту особенность, говорят, что выражение  представляет неопределенность вида
представляет неопределенность вида  .
.
5. Подобное предыдущему обстоятельство возникает, когда  ,
,  . Проиллюстрируем этот факт примерами:
. Проиллюстрируем этот факт примерами:
 ,
,  ,
,  ;
;
 ,
,  ,
,  ;
;
 ,
,  ,
, 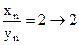 ;
;
 ,
, 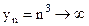 ,
,  не имеет предела.
не имеет предела.
В этом случае говорят, что выражение  является неопределенностью вида
является неопределенностью вида  .
.
6. Рассмотрим далее произведение  . Если существует отличный от нуля предел
. Если существует отличный от нуля предел  (конечный или бесконечный), а
(конечный или бесконечный), а  , то
, то  , так как обратная величина
, так как обратная величина 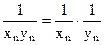 есть бесконечно малая (первый множитель имеет конечный предел, а второй стремится к нулю).
есть бесконечно малая (первый множитель имеет конечный предел, а второй стремится к нулю).
7. Если  , а
, а  , то сталкиваемся с ситуацией, которая рассматривалась в пп. 4,5.
, то сталкиваемся с ситуацией, которая рассматривалась в пп. 4,5.
В самом деле, рассмотрим примеры:
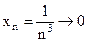 ,
,  ,
,  ;
;
 ,
, 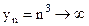 ,
, 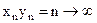 ;
;
 ,
,  ,
,  ;
;
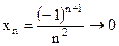 ,
,  ,
,  не имеет предела.
не имеет предела.
Рассмотренные примеры подтверждают тот факт, что выражение  есть неопределенность вида
есть неопределенность вида 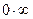 .
.
8. Можно показать, что если  , а
, а  имеет конечный предел, то
имеет конечный предел, то  .
.
9. Пусть  и
и  стремятся к бесконечности разных знаков. Этот случай также оказывается особым; различные возможности проиллюстрируем примерами:
стремятся к бесконечности разных знаков. Этот случай также оказывается особым; различные возможности проиллюстрируем примерами:
 ,
,  ,
,  ;
;
 ,
,  ,
, 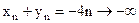 ;
;
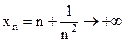 ,
,  ,
,  ;
;
 ,
,  ,
,  .
.
В силу рассмотренного говорят, что при 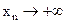 ,
, 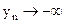 выражение
выражение  является неопределенностью вида
является неопределенностью вида  .
.
В соответствии с рассмотренным выше, мы можем сделать следующий вывод. При определении пределов суммы, произведения и частного по пределам последовательностей  и
и  , из которых они образуются, это невозможно сделать в случаях возникновения неопределенностей
, из которых они образуются, это невозможно сделать в случаях возникновения неопределенностей
 ,
,  ,
, 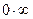 ,
,  .
.
Нужно непосредственно исследовать выражение, учитывая закон изменения последовательностей. Это исследование называется раскрытием неопределенности.

 ,
,  ,
,  , мы предполагали, что последовательности
, мы предполагали, что последовательности  и
и  имеют конечные пределы и
имеют конечные пределы и  .
. . Тогда
. Тогда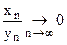 .
. , так как величина
, так как величина 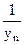 бесконечно малая (обратная бесконечно большой
бесконечно малая (обратная бесконечно большой  ).
). (конечный или бесконечный), а
(конечный или бесконечный), а , то
, то  .
. ,
, , а предел
, а предел  (так как обратное отношение
(так как обратное отношение  ).
). . В этом случае предел частного
. В этом случае предел частного 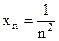 ,
,  ;
;  ,
,  .
.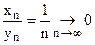 . Если же положить
. Если же положить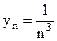 , то
, то  .
. ,
, 
 .
. ,
,  не имеет предела.
не имеет предела. и
и  .
. ,
,  . Проиллюстрируем этот факт примерами:
. Проиллюстрируем этот факт примерами: ,
,  ,
,  ;
; ,
,  ;
; ,
, 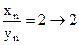 ;
; ,
, 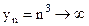 ,
,  не имеет предела.
не имеет предела. .
. , то
, то  , так как обратная величина
, так как обратная величина 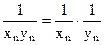 есть бесконечно малая (первый множитель имеет конечный предел, а второй стремится к нулю).
есть бесконечно малая (первый множитель имеет конечный предел, а второй стремится к нулю). , а
, а 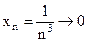 ,
,  ;
; ,
, 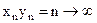 ;
; ,
,  ;
;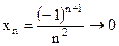 ,
,  не имеет предела.
не имеет предела.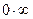 .
. .
. ,
,  ,
,  ;
; ,
,  ,
, 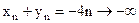 ;
;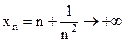 ,
,  ;
; ,
,  .
.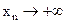 ,
, 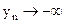 выражение
выражение  является неопределенностью вида
является неопределенностью вида  .
.


