И бесконечно больших последовательностей
Свойства бесконечно малых и бесконечно больших последовательностей сформулируем в виде теорем. Теорема 3. Сумма любого конечного числа бесконечно малых последовательностей есть бесконечно малая последовательность. ■ Докажем утверждение для двух бесконечно малых последовательностей (общий случай показывается аналогично). Пусть Теорема 4. Произведение ограниченной последовательности на бесконечно малую есть бесконечно малая. ■ Пусть Следствие 1. Произведение конечного числа бесконечно малых последовательностей есть бесконечно малая. Следствие 2. Произведение бесконечно малой последовательности на постоянную есть бесконечно малая. Теорема 5. Сумма бесконечно больших последовательностей одного знака есть бесконечно большая последовательность. ■ Пусть Последнее и означает, что Теорема 6. Произведение двух бесконечно больших последовательностей есть бесконечно большая последовательность.
|

 и
и 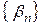 – бесконечно малые. Зададим произвольное число
– бесконечно малые. Зададим произвольное число  . По определению бесконечно малой существует номер
. По определению бесконечно малой существует номер  , начиная с которого
, начиная с которого  , и
, и  , начиная с которого
, начиная с которого 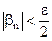 . Обозначим
. Обозначим 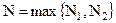 . Тогда при
. Тогда при 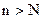 одновременно выполняются оба неравенства, так что
одновременно выполняются оба неравенства, так что 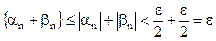 . Следовательно,
. Следовательно,  – бесконечно малая последовательность. ■
– бесконечно малая последовательность. ■ – ограниченная, а
– ограниченная, а 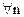
 . Выберем произвольное число
. Выберем произвольное число 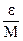 для
для  . Тогда для тех же значений n
. Тогда для тех же значений n  . Это и означает, что
. Это и означает, что 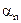 – бесконечно малая. ■
– бесконечно малая. ■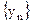 – бесконечно большие последовательности, для которых
– бесконечно большие последовательности, для которых  ,
, 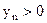 . По определению бесконечно большой последовательности для любого сколь угодно большого
. По определению бесконечно большой последовательности для любого сколь угодно большого 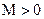 существуют такие номера
существуют такие номера 
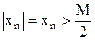 и
и 
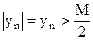 . Тогда
. Тогда 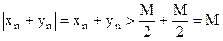 для
для 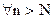 , где
, где 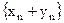 – бесконечно большая последовательность. ■
– бесконечно большая последовательность. ■


