В’язкість рідини
У реальних рідких середовищах на границях шарів, що рухаються, діють сили внутрішнього тертя. Можна навести чимало прикладів дії цих сил: вони є причиною падіння тиску вздовж судини при плині крові, саме вони визначають поведінку рідини у судині, що обертається, перешкоджують рухові тіл у рідинах тощо. Досліди свідчать про те, що сили тертя між шарами рідини, які рухаються з різними швидкостями, діють по дотичній до поверхонь цих шарів (мал. 3.7) і спрямовані таким чином, що прискорюють шар, що рухається більш повільно, і гальмують шар, який рухається швидше. Розглянемо поведінку рідини, що знаходиться між двома пластинами, одна з яких нерухома, а інша під дією прикладеної до неї сили F рівномірно рухається зі швидкістю υ; (мал. 3.7). Дія дотичного зсуваючого напруження
Рівняння (3.8), відоме як рівняння Ньютона, описує явище внутрішнього тертя. Таким чином, профіль швидкостей, який ми спостерігаємо у цьому випадку (мал. 3.8), обумовлений тим, що між шарами реальної рідини, що тече, діють сили внутрішнього тертя F, які пропорційні до площі S шарів, що дотикаються, та градієнта швидкості Розмірність коефіцієнта в’язкості h у системі СІ [ Па×с ]. Досить часто використовується ще й позасистемна одиниця в’язкості Пуаз (П), яка зв’язана з Па×с співвідношенням 1 П = 0.1 Па×с. Так, в’язкість дистильованої води при кімнатній температурі дорівнює приблизно 10–3 Па×с = 10–2 П, тобто hводи» 1 мПа×с = 1 сП. Зручно користуватися безрозмірним коефіцієнтом в’язкості, що зветься відносною в’язкістю hвідн . Відносна в’язкість дорівнює відношенню коефіцієнта в’язкості даної рідини до коефіцієнта в’язкості дистильованої води при одній і тій самій температурі:
У гідродинаміці користуються також і кінематичною в’язкістю n рідини, що являє собою відношення коефіцієнта в’язкості до густини n Кінематична в’язкість n має розмірність [ n ] = м 2/ с. В’язкість рідини є динамічна властивість, залежить від природи рідини, температури і для багатьох рідин також від умов плину. Моделі рідин. Описуючи рух рідких середовищ, використовують різні моделі рідин. Найбільш простою є модель ідеальної рідини, яка не підлягає стисненню (r = сonst) і в ній відсутні сили внутрішнього тертя (h = 0). Ця модель використовується для отримання найбільш простих рівнянь руху рідини. Неідеальні рідини, в яких сили внутрішнього тертя описуються рівнянням Ньютона, звуться ньютонівськими. Для ньютонівських рідин коефіцієнт в’язкості h залежить лише від температури та природи рідини і не залежить від умов плину. До ньютонівських рідин можна віднести воду, розчини електролітів, ртуть, гліцерин, спирти. Існують рідини, коефіцієнт в’язкості яких залежить від умов плину, а саме, змінюється із зміною швидкості деформації зсуву Описуючи динаміку руху біологічних рідин, розглядають умови їх плину і, залежно від них, обирають ту чи іншу модель рідини – від ідеальної до реальної.
|


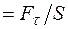 викликає деформацію зсуву, причому відносний зсув за одиницю часу
викликає деформацію зсуву, причому відносний зсув за одиницю часу 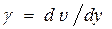 , який називають градієнтом швидкості, виявляється пропорційним до прикладеного зсувного напруження:
, який називають градієнтом швидкості, виявляється пропорційним до прикладеного зсувного напруження:
 , або
, або 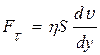 . (3.8)
. (3.8)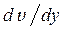 у напрямку, перпендикулярному до напрямку плину рідини. Коефіцієнт пропорційності h в рівнянні Ньютона зветься коефіцієнтом в’язкості (точніше кажучи, зсувної в’язкості) і дорівнює силі внутрішнього тертя, що діє на одиницю площі поверхні шару при градієнті швидкості, який дорівнює одиниці.
у напрямку, перпендикулярному до напрямку плину рідини. Коефіцієнт пропорційності h в рівнянні Ньютона зветься коефіцієнтом в’язкості (точніше кажучи, зсувної в’язкості) і дорівнює силі внутрішнього тертя, що діє на одиницю площі поверхні шару при градієнті швидкості, який дорівнює одиниці.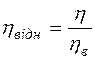 . (3.9)
. (3.9)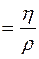 . (3.10)
. (3.10)


