Плин ньютонівської рідини по горизонтальній трубці
Формула Пуазейля. Плин в’язких рідин по циліндричних трубках має для медицини особливий інтерес. Судинна система може бути представлена сіткою циліндричних трубок різного діаметра, лінійна й об’ємна швидкості плину рідини по яких залежить не лише від властивостей рідини, а й від геометричних розмірів судин. Визначимо лінійну й об’ємну швидкості плину для стаціонарного потоку в’язкої рідини крізь судину радіусом R, довжиною L, з перепадом тиску на його кінцях P 1 – P 2 (мал. 3.16). Запишемо рівняння руху (3.24) для стаціонарного плину ньютонівської рідини, коли зовнішні сили дорівнюють нулеві, і сила тяжіння не впливає на плин рідини: – Ñ; P + f тр = 0 або Ñ; P = f тр. (3.25) Припустимо, що градієнт тиску вздовж трубки струму є постійна величина: Ñ P = (Р 2 – Р 1)/ L. Об’ємна сила тертя fтр дорівнює (3.8):
де S 1 = 2 prdx – площа бічної поверхні циліндра, S 2 = pr 2 – площа перерізу циліндра радіуса r. Підставивши ці вирази у рівняння (3.25), отримаємо диференційне рівняння, що визначає зміну швидкості рідини вздовж радіуса трубки: dυ; = – Проінтегруємо це рівняння υ; = – де сталу інтегрування С знаходимо з умови υ; = 0 на границі судини, тобто при r = R. Це дає С = υ; = З цієї формули випливає, що профіль швидкостей ньютонівської рідини в циліндричній трубці описується параболічним законом (мал. 3.17а). Формула Пуазейля дозволяє визначити об’ємну швидкість плину ньютонівської рідини. Виділимо у перерізі трубки шар рідини товщиною dr і площею dS = 2 prdr (мал. 3.17б). Об’єм рідини, що протікає крізь цю площу за одиницю часу, дорівнює dQ = υ;(r) dS = υ;(r)×2 prdr.
Мал. 3.17. Характеристики плину ньютонівської рідини по циліндричній трубці: а) профіль швидкостей; б) переріз трубки струму. Підставивши в цю формулу вираз (3.26) для швидкості і інтегруючи отримане рівняння, дістанемо формулу, що дозволяє визначити об’ємну швидкість рідини:
Помноживши об’ємну швидкість рідини на час плину, отримаємо формулу для визначення об’єму рідини V, що протікає через переріз судини за час t:
З формул (3.27) та (3.28), які звуться формулами Гагена–Пуазейля, випливає, що кількість рідини, яка протікає крізь судину, найбільш суттєво залежить від його радіуса і зменшується із зростанням в’язкості рідини. Формула (3.27), що зв’язує між собою об’ємну швидкість рідини і різницю тисків на кінцях судини, має вигляд, аналогічний закону Ома: Q = (P 1 – P 2)/ W, (3.29) тому величину W = 8 hL /(pR 4) називають гідравлічним опором.
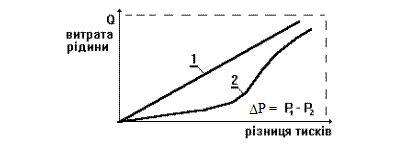
Графічні зображення зв’язку Q –D P називають діаграмами “ витрата–тиск ”.Їх вигляд для ньютонівської рідини і рідини, в’язкість якої залежить від градієнта швидкості (наприклад, для крові), подані на мал. 3.18. Мал. 3.18. Діаграми “витрата–тиск” для ньютонівської (1) та неньютонівської (2) рідин.
|

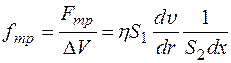 ,
, × rdr.
× rdr.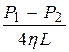 × r 2 + С,
× r 2 + С,
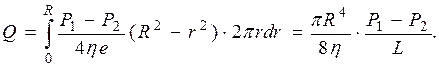 (3.27)
(3.27)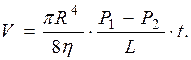 (3.28)
(3.28)