Основні рівняння руху рідини
Мал. 3.13. Лінії струму при стаціонарному (а) і турбулентному плині (б), трубка струму (в). Описуючи потік рідини, часто використовують терміни – поле швидкостей і профіль швидкостей, що являють собою відповідно значення швидкостей у всіх точках простору і точках перерізу трубки струму у фіксований момент часу. Якщо лінії струму і поле швидкостей не змінюються з часом, то рух рідини зветься стаціонарним. При стаціонарному плині траєкторії частинок залишаються незмінними. Швидкість частинки може змінюватися при її русі вздовж лінії струму, але у кожній точці лінії струму вона зберігається за величиною і напрямком. Якщо поле швидкостей і лінії струму змінюються з часом, то такий плин зветься нестаціонарним. У цьому випадку лінії струму під час плину зникають і знову з’являються, у деяких випадках за формою вони нагадують вихори (мал. 3.13б), такий плин рідини зветься турбулентним або вихровим. Рівняння нерозривності струменя. Розглянемо стаціонарний плин рідини. Позначимо через υ; середню швидкість плину рідини для довільно вибраного перерізу S трубки струму. Маса рідини, що протікає через цей переріз за одиницю часу, залишається постійною через те, що рідина не розривається і не стискається в звичайних умовах, тобто dm / dt = const. (3.15) (Якщо б ця умова не виконувалася, то тубка струму не зберігалася б постійною у просторі). Оскільки dm = Sdl = r×S×υ; = const. (3.16) Для нестисливої рідини (r = const) рівняння нерозривності струменю дає зв’язок між площиною перерізу трубки струменю і середньою швидкістю плину рідини: S × υ; = const, або для різних перерізів трубки струму (див. мал. 3.14) S 1× υ; 1 = S 2× υ; 2. (3.17) Величина Q = dV / dt = S × υ [V.P.1] [ м 3/ с ], що дорівнює об’єму рідини, який протікає через переріз трубки струму за одиницю часу, зветься об’ємною швидкістю плину рідини. При стаціонарному плині вона залишається величиною сталою. Аналогами цієї величини у фізіології є витрата крові або хвилинний об’єм крові (ХОК). Виходячи з визначення об’ємної швидкості плину рідини, хвилинний об’єм крові можна обчислити як відношення ударного об’єму крові Vуд до періоду скорочення серця Т, або добуток Vуд на частоту серцевих скорочень ЧСС = 1/ Т: ХОК = Vуд / Т = Vуд × ЧСС. Коли кров рухається по еластичних судинах, внаслідок їх деформації при зміні тиску лінії струму не залишаються постійними. У цьому випадку рівняння нерозривності струменю може бути подано таким чином: dV / dt = Q 1(t) – Q 2(t), або де Q 1(t) та Q 2(t) – відповідно приплив та відток крові для ділянки судини. Ці рівняння будуть в подальшому використані при вивченні фізичних основ реографії.
Мал. 3.14. Трубка струму. Рівняння Бернуллі. Розглянемо стаціонарний плин ідеальної рідини. Виділимо у просторі трубку струму (мал. 3.14) і розглянемо енергію малого елемента об’єму рідини з масою D m = r D V, що протікає через переріз трубки струму за деякий час. Оскільки рідина є ідеальною і робота сил тертя дорівнює нулю, то повна енергія деякого елементу об’єму рідини у цьому випадку буде залишатися величиною сталою при русі вздовж трубки струму: E = Eк + Eп + Ecт = const, (3.19) де Ек = D m × υ;2/2 – кінетична енергія, Еп = D mgh – потенціальна енергія, а Ecт = Р ×D V – потенціальна енергія виділеного об’єму рідини. Підставляючи ці вирази у формулу (3.19) і вводячи об’ємну густину енергії w = E /D V, отримаємо рівняння Бернуллі, котре являє собою закон збереження енергії для одиниці об’єму рідини, що рухається
Таким чином, фізичний зміст рівняння Бернуллі полягає в тому, що об’ємна густина енергії w ідеальної рідини при її стаціонарному плині залишається величиною сталою. Зауважимо, що розмірність об’ємної густини енергії дорівнює [ w ] = [ E ]/[D V ] = Дж / м 3= Н / м 2, тобто вона збігається з розмірністю тиску [ p ] = Па = Н / м 2. Тому в гідравліці компоненти об’ємної густини енергії w називають: rυ;2/2 – динамічним, rgh – гідростатичним та Р – статичним тисками. У цьому випадку рівняння Бернуллі свідчить про те, що сумарний тиск залишається постійним вздовж трубки струму при стаціонарному плині ідеальної рідини.
Мал. 3.15. Об’ємна енергія крові: w вен – у венозному руслі; w арт – у артеріальному руслі; їх різниця wc = w арт – w вен. Коли кров рухається по судинному руслу, величина об’ємної густини енергії різко змінюється при переході з венозного русла до артеріального (мал. 3.15). Ця зміна обумовлена діяльністю серця як насоса. Насосна функція серця полягає у змініоб’ємної густини енергії крові. Насосну функцію серця можна характеризувати різницею об’ємних густин енергії на вході та виході серця, тобто величиною wc = wарт – wвен. Розрахунок цих величин за формулою (3.20) свідчить про те, що більш як 95% від величини wс припадає на потенціальну енергію стисненої рідини в аорті, яка, в свою чергу, визначається величиною середнього артеріального тиску. Отже, величина артеріального тиску дозволяє судити про насосну функцію серця й енергію крові на виході серця, за рахунок якої відбувається її подальший рух по судинному руслу. Зауважимо, що у всіх теплокровних середнє значення артеріального тиску одне і те ж, порядку 90–100 мм Hg, у той час, як інші найважливіші показники системи кровообігу (такі, як хвилинний об’єм, частота серцевих скорочень) значно відрізняються. Більш того, в організмі існує спеціальна система слідкування за артеріальним тиском, а точніше – за об’ємною густиною енергії крові. Саме її підтримка на певному рівні дозволяє забезпечити рух крові крізь капіляри з оптимальною швидкістю, при якій відбувається рівномірна віддача кисню оточуючим тканинам (незалежно від того, яка їх кількість включена до роботи і який хвилинний об’єм протікає крізь них). З наведеного вище можна зробити висновок, що кількість енергії, що її передає серце одиниці об’єму крові, є однією з найважливіших констант організму. Спеціальні регуляторні механізми серця забезпечують саме такий режим скорочення міокарда, за якого при різних навантаженнях серце було б здатне підтримувати на певному рівні об’ємну густину енергії потоку крові, витрачаючи при цьому мінімум хімічної енергії при скороченні міокарда. Рівняння руху і рівноваги рідини. Виділимо у рідині елементарний об’єм D V циліндричної форми з перерізом S і довжиною D х (мал. 3.16). За другим законом Ньютона:
або для об’ємних сил:
Розглянемо сили, що діють на елемент об’єму рідини. Результуюча сила тиску дорівнює F = S [ P (x) – P (x + dx)] = – SdP, тоді як об’ємна сила тиску (сила, що діє на одиницю об’єму) є
Проводячи аналогічний розгляд для у, z -компонент сил, отримаємо:
де Ñ;– символ градієнта (так званий “оператор набла”). З рівняння (3.22) випливає, що об’ємна результуюча сила тиску за модулем дорівнює градієнту тиску.
Мал. 3.16. Сили, що діють на елемент об’єму рідини. Рівняння руху рідини (3.4) з урахуванням інших об’ємних сил, а саме, сили тертя fтр, сили тяжіння rg, інших зовнішніх сил fзовн, можна записати у вигляді: r × d υ;/ dt = – Ñ; P + f тр + r g + f зовн. (3.23) Якщо сила тиску врівноважується іншими силами за умови, що Ñ; Р + f тр + r g + f зовн = 0. (3.24) Аналогічним рівнянням описують і рівноважний стан рідини, коли рідина знаходиться у спокої, тобто швидкість
|


 , r – густина середовища), розглянути сили, що діють на нього і записати рівняння статики (рівноваги) чи динаміки. При русі у просторі кожний такий елементарний об’єм рухається вздовж деякої траєкторії – лінії струму (мал. 3.13а,б). Дотична до будь-якої точки лінії струму збігається з напрямом вектора швидкості частинки у цій точці. Виділимо у просторі замкнений контур S. Всі лінії струму, що проходять крізь цей контур, утворюють трубку струму. Таким чином, трубка струму являє собою частину потоку рідини, обмежену лініями струму (мал. 3.13в).
, r – густина середовища), розглянути сили, що діють на нього і записати рівняння статики (рівноваги) чи динаміки. При русі у просторі кожний такий елементарний об’єм рухається вздовж деякої траєкторії – лінії струму (мал. 3.13а,б). Дотична до будь-якої точки лінії струму збігається з напрямом вектора швидкості частинки у цій точці. Виділимо у просторі замкнений контур S. Всі лінії струму, що проходять крізь цей контур, утворюють трубку струму. Таким чином, трубка струму являє собою частину потоку рідини, обмежену лініями струму (мал. 3.13в). ×υ;× dt, з рівняння (3.15) отримаємо:
×υ;× dt, з рівняння (3.15) отримаємо: , (3.18)
, (3.18)
 . (3.20)
. (3.20)
 ,
, . (3.21)
. (3.21)
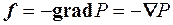 , (3.22)
, (3.22)
 , то
, то .
.


