Пасивний транспорт незаряджених молекул
Математичний опис процесу дифузії було дано Фіком. Згідно з рівнянням Фіка густина потоку Ф дифундуючої речовини визначається виразом: Ф = –Ddc/dx. (6.11) Вираз (6.11) – це закон Фіка для вільної дифузії, де Розглянемо пасивний транспорт незаряджених молекул крізь мембрану. Розподіл концентрацій молекул дифундуючої речовини при переході через мембрану показано на мал. 6.24, де використані такі позначення: ce, ci – концентрації дифундуючих частинок у водному середовищі зовні і в клітині; cме і cмi – концентрації частинок у самій мембрані біля зовнішньої і внутрішньої її поверхонь.
З наведеного малюнку видно, що концентрація зовні клітини ce перевищує концентрацію у клітині ci, а в самій мембрані змінюється за лінійним законом, тобто dc/dx = const і дорівнює: dc/dx = – (cме – cмi)/L, (6.12) де L – товщина мембрани. Це є, звичайно, припущенням. Концентрація частинок на поверхнях мембрани зазнає стрибок внаслідок різної розчинності речовини у водній фазі і пристінному шарі всередині мембрани. Звичайно існує пропорційний зв’язок: cме / ce = cмi / ci = K, (6.13) де К – коефіцієнт розподілу речовини між мембраною та водною фазою. Рівняння (6.11) з урахуванням (6.12) і (6.13) набуває вигляду:
де P = D×K/L – коефіцієнт проникності мембрани. Таким чином, При русі речовини крізь мембрану, частинки вимушені долати не лише гідрофобний шар ліпідів, а й нерухомі шари Потоки через кожний з перелічених шарів:
де Pe, Рм, Рі – коефіцієнти проникності відповідних бар’єрів. Поділимо рівняння (6.15) для потоків Фe, Фм, Фі на відповідні коефіцієнти проникності і додамо праві і ліві частини:
У стаціонарному стані не відбувається накопичення речовини, тобто c ¹ f (t), а тому всі потоки рівні між собою: Фe = Фм = Фі =Ф. З іншого боку, для всієї системи в цілому
де Р – коефіцієнт проникності всієї системи. З рівняння (6.17) маємо:
Тоді з рівнянь (6.16) і (6.18) випливає, що
Величина 1 /Р – опір потоку речовини, який дорівнює сумі опорів складових шарів. Опір примембранних шарів пропорційний до товщини цих шарів, дійсно:
де K = 1 для водних шарів; Di – коефіцієнт дифузії речовини у воді. Таким чином, проникність мембрани залежить від руху протоплазми у міжклітинному середовищі і всередині клітини, який спричиняє перемішування рідини і зменшення товщини примембранних нерухомих шарів. Пригнічування процесів життєдіяльності клітин призводить до збільшення опору і, як наслідок, до гальмування процесів пасивного переносу речовин крізь мембранні системи.
|

 – кількість частинок речовини (молекул), що перетинають одиничну площину за одиницю часу, D – коефіцієнт дифузії, dc/dx – градієнт концентрації дифундуючої речовини. Для газів і розбавлених розчинів коефіцієнт дифузії може бути визначений за формулою
– кількість частинок речовини (молекул), що перетинають одиничну площину за одиницю часу, D – коефіцієнт дифузії, dc/dx – градієнт концентрації дифундуючої речовини. Для газів і розбавлених розчинів коефіцієнт дифузії може бути визначений за формулою  , де
, де  – середня швидкість руху молекул
– середня швидкість руху молекул  – середня довжина вільного пробігу молекул. Знак “–” вказує на те, що потік речовини Ф напрямлений в бік зменшення її концентрації, тобто в бік, протилежний напрямку градієнта концентрації (мал. 6.23).
– середня довжина вільного пробігу молекул. Знак “–” вказує на те, що потік речовини Ф напрямлений в бік зменшення її концентрації, тобто в бік, протилежний напрямку градієнта концентрації (мал. 6.23).
 , (6.14)
, (6.14) – рівняння, що описує пасивний транспорт незаряджених молекул крізь мембрану.
– рівняння, що описує пасивний транспорт незаряджених молекул крізь мембрану.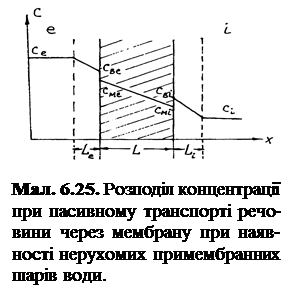 води, що прилягають до мембрани (примембранні шари). Нехай речовина рухається всередину клітини з водного розчину з концентрацією сe до водного розчину з концентрацією сi. При цьому частинки повинні долати три дифузійні бар’єри: зовнішній примембранний шар води, саму мембрану і внутрішній примембранний шар води (мал. 6.25).
води, що прилягають до мембрани (примембранні шари). Нехай речовина рухається всередину клітини з водного розчину з концентрацією сe до водного розчину з концентрацією сi. При цьому частинки повинні долати три дифузійні бар’єри: зовнішній примембранний шар води, саму мембрану і внутрішній примембранний шар води (мал. 6.25). (6.15)
(6.15) . (6.16)
. (6.16) . (6.18)
. (6.18) .
. ,
,


