Пасивний транспорт іонів
У відсутності градієнта концентрації перенос заряджених частинок (іонів) може відбуватися при наявності електричного поля, тобто градієнта електричного потенціалу (E = – dj /dx). Густина електричного струму іонів за законом Ома:
де g – коефіцієнт електропровідності середовища. Як відомо, густина електричного струму дорівнює: j = qcυ, (6.20) де с – кількість носіїв заряду (іонів) в одиниці об’єму середовища: υ – швидкість, з якою рухаються носії (іони) під впливом електричного поля; q – заряд носія (іона). Оскільки υ = bE = – bdj /dx, де b – рухливість іона, a
Згідно з визначенням густини струму
де
Заряд dQ, що проходить через площину S за час dt:
dQ = q×dN, (6.24)
де dN – кількість іонів, що перетинають площину S за час dt. Об’єднавши вирази (6.22), (6.23) і (6.24), одержимо:
Згідно з визначенням густини потоку речовини:
Порівнюючи (6.25) і (6.26) одержимо вираз для густини потоку іонів, обумовленого градієнтом електричного потенціалу:
Рухливість іона пов’язана з коефіцієнтом дифузії співвідношенням Ейнштейна
де F – число Фарадея, Т – абсолютна температура, R – газова стала. Тоді (6.27) набуває вигляду:
При наявності як градієнта концентрації іонів, так і градієнта потенціалу електричного поля, густина потоку іонів дорівнює:
Рівняння (6.28) відоме як електродифузійне рівняння Нернста-Планка, що описує пасивний транспорт заряджених частинок (іонів). Виконавши деякі елементарні перетворення, рівняння Нернста-Планка можна подати в іншому вигляді:
Тут враховано ту обставину, що (1 /с) dc/dx = (d ln c) /dx. Крім того, під знак похідної (градієнта) внесено постійну величину – хімічний потенціал розчинника
зветься електрохімічним потенціалом
Рівняння (6.30) відоме як рівняння Теорелла. Згідно з ним, рушійною силою пасивного транспорту іонів виступає градієнт електрохімічного потенціалу, у той час як рушійною силою пасивного транспорту незаряджених молекул є градієнт концентрації.
Мал. 6.26. Види пасивного і активного транспорту через мембрану: 1 – проста дифузія через мембрану; 2 – дифузія через канали; 3 – дифузія за допомогою переносників; 4 – активний транспорт. Процес простої (або звичайної) дифузії відбувається повільно і погано контролюється клітиною. За таким механізмом здійснюється транспорт кисню, вуглекислого газу та шкідливих для клітини речовин (наприклад, ядів). При звичайній дифузії молекула дифундуючої речовини рухається крізь мембрану без утворення комплексів з іншими молекулами. Для більш швидкого переносу речовин, необхідних для життєдіяльності клітин, в ході еволюції виробились інші типи пасивної дифузії: перенос через канали (пори) і перенос за допомогою переносників. Ці типи дифузії відомі під назвою полегшеної дифузії (мал. 6.26). Розглянемо більш детально пасивний транспорт речовин крізь канали. Канали – це білкові утворення, що мають діаметр 6–10 Å (1 Å (ангстрем) = 10–10 м). Згідно з деякими даними, білкові канали покривають ~ 0.1% поверхні мембрани. Слід підкреслити, що канали – не статичні, а динамічні утворення. Один з механізмів їх утворення – процес латеральної дифузії. Коефіцієнт проникності мембрани при пасивному транспорті через канали:
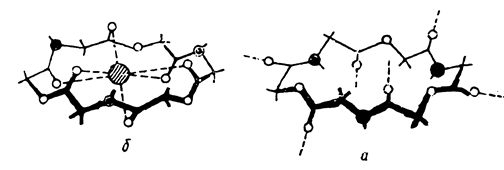
де п – кількість каналів на одиницю площі мембрани, r – радіус каналу, L – довжина каналу (товщина мембрани), D – коефіцієнт дифузії речовини у воді. Згідно з гіпотезою Мулінза найкраще проходять крізь канали ті іони, радіус яких в оточенні одного шару молекул води близький до радіуса каналу. Швидкість пасивного транспорту крізь мембрани збільшується на декілька порядків у присутності переносників – молекул, що володіють дуже високим рівнем селективності. Наприклад, переносник, який полегшує транспорт глюкози крізь мембрану, ніяк не впливає на транспорт амінокислот. Найбільш детально полегшений транспорт крізь біологічні мембрани було вивчено на прикладі переносу іонів іонофорними антибіотиками типу валіноміцину. Було встановлено, що валіноміцин вибірково збільшує проникність мембран для іонів К+. Шість карбонільних груп валіноміцину формують порожнину, в яку потрапляє іон К+. У вільній молекулі валіноміцину атоми складноефірних карбонільних груп спрямовані до зовнішньої поверхні молекули. При утворенні комплексу з іонами К+ у молекулі виникають додаткові іон-дипольні взаємодії з атомами кисню карбонільних груп. Молекула набуває форми браслету, діаметром близько 8 Å, у центрі якого розташовується іон К+. На мал. 6.27 показано конформаційну зміну молекули валіноміцину при створенні комплексу з іоном К+. Іони Na+ надто великі для порожнини у молекулі валіноміцину, внаслідок чого різниця у проникностях для іонів К+ і Na+ становить:
Мал. 6.27. Просторова структура валіноміцину (а) та його комплексу з іоном (б). Транспорт за допомогою переносників може відбуватись внаслідок дифузії переносника разом з речовиною (рухомий переносник) (мал. 6.28а), а також і шляхом естафетної передачі від однієї молекули переносника до іншої (. 6.28б).
Мал. 6.28. Транспорт іонів за участю переносників: а) рухомий переносник, б) естафетний перенос. Для пасивного транспорту за допомогою переносників характерний ефект концентраційного насичення швидкості переносу: зі збільшенням концентрації швидкість переносу сповільнюється, тому що всі переносники виявляються пов’язаними з певною долею іонів.
|

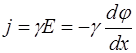 , (6.19)
, (6.19) , де z – валентність іона, то вираз для густини струму набуває вигляду:
, де z – валентність іона, то вираз для густини струму набуває вигляду: . (6.21)
. (6.21) , (6.22)
, (6.22)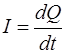 . (6.23)
. (6.23) . (6.25)
. (6.25) . (6.26)
. (6.26) . (6.27)
. (6.27) ,
, .
. . (6.28)
. (6.28) (6.29)
(6.29) , який є однаковим по обидві сторони мембрани і тому не залежить від координати, по якій виконується диференціювання. Величина, яка стоїть у дужках, тобто
, який є однаковим по обидві сторони мембрани і тому не залежить від координати, по якій виконується диференціювання. Величина, яка стоїть у дужках, тобто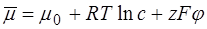
 (див. розділ 7.1). Його фізичний зміст полягає в тому, що він визначає вільну енергію Гібса з розрахунку на один моль у присутності розчиненої речовини і електричного поля. Другий доданок RT ln С визначає вклад розчиненої речовини (осмотичний вклад) в електрохімічний потенціал, у той час як останній доданок ZFj характеризує вклад електричного поля. Враховуючи означення електрохімічного потенціалу, рівняння (6.29) можна подати у вигляді:
(див. розділ 7.1). Його фізичний зміст полягає в тому, що він визначає вільну енергію Гібса з розрахунку на один моль у присутності розчиненої речовини і електричного поля. Другий доданок RT ln С визначає вклад розчиненої речовини (осмотичний вклад) в електрохімічний потенціал, у той час як останній доданок ZFj характеризує вклад електричного поля. Враховуючи означення електрохімічного потенціалу, рівняння (6.29) можна подати у вигляді: . (6.30)
. (6.30)
 ,
, . Таким чином, основою селективності при переносі іонів за допомогою переносників, так само, як і при переносі через канали, є принцип структурної відповідності.
. Таким чином, основою селективності при переносі іонів за допомогою переносників, так само, як і при переносі через канали, є принцип структурної відповідності.