Основне рiвняння квантової механiки – рiвняння Шредiнгера
Рiвняння, що описує рух мiкрочастинки, повинне вiдтворювати її хвильовi властивостi, тобто повинне бути подiбним до хвильового рiвняння, що описує розповсюдження оптичних або акустичних хвиль (див. рівняння (3.58) в першому томі):
Ми можемо мiркувати таким чином: якщо мiкрочастинка, яка рухається, має хвильовi властивостi i може бути охарактеризована довжиною хвилi, то її стан можна описати за допомогою деякої функцiї Y, яка повинна задовольняти хвильове рiвняння (9.8), тобто:
Функцiя, що задовольняє хвильове рiвняння, може бути подана у такому виглядi: Y = y (х) sin w t. Знайдемо відповідні частиннi похiднi, а саме:
i пiдставимо їх в рiвняння (9.9), що в результатi дає
Враховуючи зв’язок мiж частотою і періодом
Тодi рiвняння (9.9) набуває такий вигляд:
де Еk – кiнетична енергiя частинки. Рiвняння (9.10) описує одновимiрний рух частинки. У випадку, коли частинка рухається в тривимірному просторi, рiвняння (9.10) матиме вигляд:
або
де Якщо частинка рухається в силовому полi, то її повна енергiя дорiвнює сумi кiнетичної та потенцiальної енергiй: Е = Ek + En , звiдки Еk = Е – Еn. У цьому випадку рiвняння (9.12) записується таким чином:
Рiвняння (9.13) – стацiонарне рiвняння Шредiнгера, запропоноване ним у 1926 році. Це рiвняння описує поведiнку електрона в атомi (тобто електрона, що рухається в полi ядра). Хвильова функцiя y (x, y, z), яка є розв’язком рiвняння Шредiнгера, не залежить вiд часу і характеризує стацiонарнi стани системи. Спiввiдношення мiж y- функцiєю та частинкою, яку вона описує, аналогiчне спiввiдношенню мiж свiтловою хвилею та фотоном. Квадрат амплiтуди свiтлової хвилi А 2 визначає ймовiрнiсть попадання фотона у вiдповiдну точку простору. Як показав М. Борн, квадрат амплiтуди хвильової функцiї | y |2 характеризує ймовiрнiсть знаходження частинки в данiй точцi простору, а | y |2 dv – ймовiрнiсть знаходження частинки в елементi об’єму dv. Таким чином, фiзичний змiст має не сама хвильова функцiя, а її квадрат. Слiд відзначити, що, на вiдмiну вiд оптичних хвиль, y- функцiя характеризує не електромагнiтну хвилю, а хвилю ймовiрностi.
|

 . (9.8)
. (9.8) . (9.9)
. (9.9)
 .
. , а також зв’язок мiж довжиною хвилі, швидкістю і періодом
, а також зв’язок мiж довжиною хвилі, швидкістю і періодом  T i формулу (9.4) для довжини хвилі де Бройля, вiдношення w 2/ u 2 можна подати таким чином:
T i формулу (9.4) для довжини хвилі де Бройля, вiдношення w 2/ u 2 можна подати таким чином:
 (9.10)
(9.10) , (9.11)
, (9.11) (9.12)
(9.12)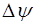 – так званий оператор Лапласа, який діє на хвильову функцію і дорівнює сумі всіх других просторових похідних від
– так званий оператор Лапласа, який діє на хвильову функцію і дорівнює сумі всіх других просторових похідних від  . Рiвняння (9.12) описує рух вiльної частинки.
. Рiвняння (9.12) описує рух вiльної частинки. (9.13)
(9.13)


