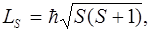Рiвняння Шредiнгера для атома водню
Потенцiальна енергiя системи електрон-ядро в атомі водню має вигляд кулонівської потенціальної енергії
З врахуванням цього виразу запишемо рiвняння Шредiнгера для найпростiшої атомної системи – атома водню:
Фiзичний змiст | y |2 накладає на y- функцiю вимоги скiнченностi, однозначностi та неперервностi. Рiвняння Шредiнгера для атома водню має розв’язок, що задовольняє вище перерахованим вимогам: при Е > 0 y -функцiя описує стан електрона, що є вільним і вже не належить даному атому, а при Е < 0 y -функція описує стан електрона всерединi атома. В останньому випадку повна енергiя системи дорiвнює:
Хвильова функцiя, що є розв’язком рiвняння Шредiнгера, містить в собі три цiлочисельнi параметри, якi називаються квантовими числами. Головне квантове число n, що характеризує енергiю електрона i розмiри його орбiталi (розмiри електронної хмари), може приймати значення:
де К, L, M, N – позначення вiдповiдних енергетичних рiвнiв. Орбiтальне квантове число l, характеризує величину моменту кiлькостi руху, тобто характеризує форму орбiталi:
де l може набувати значення
Вiдповiднi форми орбiталей наведенi на мал. 9.4.
Мал. 9.4. Різні форми електронних орбіталей. При наявностi зовнiшнього магнiтного поля можливi лише певнi орiєнтацiї вектора момента кiлькостi руху L (мал. 9.5) до напрямку зовнiшнього поля, а саме лише тi, для яких проекцiя L на напрям поля дорiвнює:
де ml =
де S – спiнове квантове число, для електрона S = 1/2. При наявностi зовнiшнього магнітного поля В проекцiя LsZ на його напрямок може набувати значення:
де mS = +1/2, –1/2. Таким чином, магнiтне спiнове число mS визначає проекцiю LSZ на напрямок магнітного поля.
|
.
(9.14)
.
.
Магнiтне квантове число ml визначає просторову орiєнтацiю орбiталей. Виявляється, що перерахованi вище квантовi числа n, l, ml не повнiстю характеризують стан електрона. Iснує ще одне квантове число, необхiднiсть введення якого не витiкає з рiвняння Шредiнгера. Згiдно з уявленнями квантової механiки, електрон має власний момент кiлькостi руху – спiн, величина якого дорівнює:
