Многоугольники. Свойства выпуклых многоугольников. Принадлежность точки многоугольнику.
Рисунок 8 – Схема разомкнутого нивелирного хода
H41 – отметка исходного репера рп41 в начале хода; для всех вариантов H41 = 100, 000 м; H42 – отметка исходного репера рп42 в конце хода; она вычисляется по номеру варианта N по формулам: вариант N чётный
вариант N нечётный
здесь e – единицы, а d – десятки номера варианта N. Длины секций в километрах и измеренные превышения по ним одинаковы для всех вариантов и приведены в таблице 9.
Таблица 9 – значения измеренных превышений и длин секций
Порядок обработки хода:
1) Вычисление высотной невязки хода где с сравнение её с допустимым значение для технического нивелирования 2) Вычисление поправок в измеренные превышения
поправки нужно округлять до миллиметров (или в метрах – до третьего знака после запятой); 3) Проверка контроля 4) Вычисление исправленных превышений 5) Вычисление отметок реперов Пример обработки хода технического нивелирования приведён в таблице 9.
Таблица 9 – Обработка хода технического нивелирования
Многоугольники. Свойства выпуклых многоугольников. Принадлежность точки многоугольнику. Многоугольником (полигоном) обычно называется замкнутая ломаная линия, то есть линия, которая получается, если взять n любых точек A1, A2,..., An и соединить прямолинейным отрезком каждую из них с последующей, а последнюю - с первой. Точки A1, A2,..., An называются вершинами многоугольника, а отрезки A1A2, A2A3..., An-1An, AnA1-сторонами (ребрами). Многоугольник называется простым, если он не пересекает самого себя. Многоугольник называется плоским, если все его вершины лежат в одной плоскости. Простой плоский многоугольник охватывает односвязную область плоскости, которая считается его внутренней частью. Далее под многоугольником мы будем понимать простой плоский многоугольник вместе с его внутренней частью. То есть будем говорить, что точка принадлежит многоугольнику, если она принадлежит его границе или внутренней части. Многоугольник называется выпуклым, если 1) отрезок, соединяющий его две любые точки целиком находится внутри многоугольника или 2) отрезок, соединяющий его две любые его вершины целиком находится внутри многоугольника или 3) многоугольник целиком расположен в одной полуплоскости относительно любого из его ребер или 4) Любая прямая, не проходящая через вершину, пересекает ребра 0 или 2 раза. или 5) Любой луч, исходящий из любой внутренней точки многоугольника либо пересекает ребра ровно 1 раз, либо проходит через вершину. или 6) Векторные произведения всех смежных ребер, взятых в одном порядке обхода, или все неотрицательны или все неположительны, но не равны нулю одновременно. Условия 1-6 эквивалентны. Любой треугольник является выпуклым. Любой многоугольник можно представить в виде совокупности выпуклых многоугольников, не имеющих общих внутренних точек. Разбиение многоугольника на треугольники называется триангуляцией многоугольника. Точка принадлежит выпуклому многоугольнику, если она лежит по одну сторону от всех его ребер, взятых в одном порядке обхода. Точка принадлежит произвольному многоугольнику, если произвольный луч, исходящий из нее и не проходящий через вершину пересекает ребра нечетное число раз. На практике удобно выбрать фиксированное относительно системы плоских декартовых координат направление луча и не ограничивать себя требованием непересечения вершин. Для горизонтального луча следует не учитывать прохождения через горизонтальные ребра, а прохождение через вершину считать пересечением только с тем ребром, для которого она является верхней, так как если ребра, выходящие из вершины лежат по одну сторону луча, то эта вершина не влияет на принадлежность точки многоугольнику.
|
,
;
,
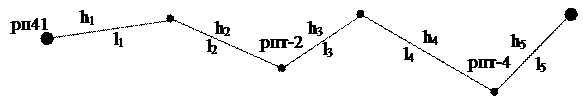
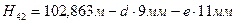- теоретическая сумма превышений, 
;
;
;
;
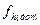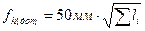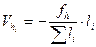; если контроль не выполняется хотя бы на 1 миллиметр, то нужно исправить одну или несколько поправок на 1 миллиметр, начиная с самой длинной секции, до абсолютного выполнения контроля;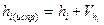
;
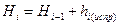; вычисленное значение отметки репера рп42 должно в точности совпадать с его заданным значением.
(м)
(м)
;
;
.
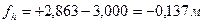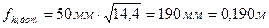