Основные виды проекций.

В системах геометрического моделирования часто используется параллельная проекция. Точки объекта проецируются на картинную плоскость с помощью пучка параллельных некоторому направлению V лучей.

Преобразование описаний объектов на плоскость наблюдения вдоль линий, параллельных вектору нормали к плоскости наблюдения N, называется ортогональной проекцией (ортографической). В результате получается параллельная проекция, в которой лини и проекции перпендикулярны плоскости наблюдения.

Перспективное изображение широко применяется в художественном, архитектурном и техническом графическом моделировании для создания представления об удаленности объектов от наблюдателя.

Одним из видов перспективного проецирования, часто используемым в графике, является одноточечная перспективная проекция, задаваемая положением центра проекции - точки схода прямых, перпендикулярных картинной плоскости до преобразования. В часто реализуемом случае расположения наблюдателя в центре проекции, центр проекции называют точкой зрения. Преобразование центрального проецирования переводит пучок параллельных прямых в пучок с общей точкой пересечения. На рисунке точка M₁(x₁, y₁, z₁) переходит в M₂(x₂, y₂, z₂) по следующему закону:

,

, (2.1)

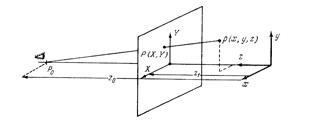Поскольку практически все доступные устройства вывода графической информации являются плоскими, в машинной графике необходимо решать задачу получения проекции пространственного изображения на картинную плоскость. Пусть точка схода P₀(0, 0, z₀) расположена на оси OZ, а картинная плоскость z1=const перпендикулярна оптической оси (т. е. оптическая ось совпадает c OZ), тогда точка P(x, y, z) проецируется из мировой системы координат xyz в плоские координаты XY на картинной плоскости.

, (2.2)

Недостатком соотношений 2.1 и 2.2 является их нелинейность. Она может быть устранена введением однородных координат (X, Y, Z, W).