Простая модель освещения.
Следующий шаг к построению фотореалистичного изображения – моделирование освещения. Рассмотрим простую модель освещения для сцены, состоящей из одного непрозрачного выпуклого многогранника и одного источника света, учитывающую рассеянный свет, диффузное и зеркальное отражение. Интенсивность отраженного света в некоторой точке будем рассчитывать по формуле I = Ia+Id+Is (4.3) где Ia – интенсивность отраженного рассеянного (ambient) света, Id - интенсивность диффузно (diffuse) отраженного света, Is - интенсивность зеркально (specular) отраженного света. Единичная интенсивность соответствует белому свету, нулевая – отсутствию света. Рассеянный свет возникает за счет многократного отражения света от предметов сцены. Он падает с равной интенсивностью со всех сторон и не имеет какого-либо локализованного источника. Интенсивность отраженного рассеянного света рассчитывается по простой формуле:
Ia = ka*Ia0 0 < ka< 1 (4.4)
где Ia0 – интенсивность рассеянного света, ka – коэффициент диффузного отражения рассеянного света. Диффузно отраженный свет точечного источника рассеивается равномерно по всем направлениям. Его интенсивность пропорциональна косинусу угла между направлением на источник света L и нормалью к поверхности N (закон косинусов Ламберта) и обратно пропорциональна квадрату расстояния d от точки на полигоне до источника света. На практике, вместо квадратичного затухания часто используют линейное.
где IL – интенсивность точечного источника света, kd – коэффициент диффузного отражения, K – постоянная затухания, обычно подбираемая экспериментально, вектора L и N предполагаются нормированными.
где ks – коэффициент зеркального отражения, n-степень, аппроксимирующая пространственное распределение зеркально отраженного света (б о льшие значения n соответствуют более блестящим поверхностям, дающим сфокусированное отражение – полированный металл и т. п., меньшие значения n соответствуют шероховатым поверхностям, например - мрамор), вектора L и N предполагаются нормированными.
24. Вычисление освещённости. Простая модель освещения. Идея метода. Достоинства и недостатки. До сих пор мы рассматривали освещение ахроматической поверхности ахроматическим светом. Простая модель освещения позволяет учитывать цвет как источника, так и поверхности. Цвета рассеянного света Ca, отраженного света С, источника Cl и поверхности Cd задаются точками в цветовом кубе RGB со стороной 1. Ca = (CaR, CaG, CaB); C = (CR, CG, CB); Cl = (ClR, ClG, ClB); Cd = (CdR, CdG, CdB). Координаты представляют собой интенсивности базовых цветов: (1, 1, 1) соответствуют белому цвету, (0, 0, 1) – синему (blue), (0, 1, 0) – зеленому (green), (1, 0, 0) – красному (red), (0, 0, 0) – черному. При диффузном отражении и отражении рассеянного света, цветовые координаты отраженного луча определяются произведением соответствующих цветовых координат падающего цвета и цвета поверхности. При зеркальном отражении цвет отраженного света определяется только цветом источника. Таким образом, имеют место следующие соотношения: CR = ka*CaR*CdR + = ka*CaR*CdR+ CG= ka*CaG*CdG+ CB= ka*CaB*CdB+ Простая модель освещения предполагает вычисление цвета одной точки полигона и закраску этим цветом всего полигона, что не всегда обеспечивает реалистичность изображения (например, в случае больших полигонов, или криволинейных поверхностей, аппроксимированных полигональными сетками). При оптимальном подборе величины разбиения эта модель позволяет достичь компромисса между качеством изображения и быстродействием. Более сложные модели закраски (например, Гуро или Фонга) в сочетании с методами трассировки лучей позволяют достичь большей степени реалистичности за счет интерполяции значений интенсивности (Гуро) или нормали (Фонг) внутри полигона, что требует дополнительных вычислений. 25. Вычисление освещённости. Модель Гуро. Идея метода. Достоинства и недостатки. Метод Гуро, изобретенный еще в 1971 г. и названный так по имени автора, был предназначен для устранения «угловатости», характерной для плоского затенения, и создания иллюзии кривизны плоского объекта. Закраска по методу Гуро выполняется на основе результатов, полученных при плоской закраске. Расчет освещенности по методу Гуро выполняется в два этапа. Сначала вычисляются значения освещенности на ребрах грани (как среднее арифметическое освещенности для смежных граней). На втором этапе выполняется линейная интерполяция освещенности вдоль параллельных линий от одного ребра к другому внутри грани. Линейный характер изменения освещенности вдоль линии позволяет составить простые и эффективные алгоритмы затенения по методу Гуро, не требующие значительных вычислительных затрат. Интерполяции может подвергаться не только освещенность, но и цвет. В игровых ЗD-акселераторах затенение Гуро является наиболее распространенным приемом, позволяющим быстро и легко устранить дефекты, полученные в результате тесселяции (разбиения на полигоны) поверхности объекта. Метод Гуро применим только для небольших граней, расположенных на значительном расстоянии от источника света. Если же размер грани достаточно велик, то расстояние от источника света до ее центра будет значительно меньше, чем до ее вершин, и, согласно закону освещенности, центр грани должен быть освещен сильнее ребер. Однако модель изменения освещенности, принятая в методе Гуро, предполагает линейное изменение яркости в пределах грани и не позволяет сделать середину грани ярче, чем ее края. В итоге на изображении появляются участки с неестественной освещенностью. 26. Вычисление освещённости. Модель Фонга. Идея метода. Достоинства и недостатки. От недостатка, присущего методу Гуро, свободна закраска Фонга. Данный метод, как и два предыдущих, предполагает постоянство расстояния от источника света до каждой из вершин грани, но учитывает изменение угла падения света для различных точек грани (в идеале — для всех точек, как минимум — для вершин грани). Это позволяет более корректно рассчитать освещенность грани, особенно в том случае, когда источник света расположен на небольшом расстоянии от нее. Другой важной особенностью закраски по методу Фонга является то, что для каждой точки грани используется своя «нормаль», направление которой может отличаться от направления истинной нормали к грани. Строго говоря, эти «нормали» не являются таковыми в полном смысле. Всем известно, что векторы, перпендикулярные одной плоскости (в данном случае — грани), должны быть параллельны друг другу. Однако «нормалью» эти векторы названы не случайно: согласно методу Фонга, они ориентируются таким образом, что являются нормалями некоторой воображаемой выпуклой или вогнутой поверхности, которой принадлежат вершины грани. В дальнейшем, при расчете освещенности каждой точки грани, в соотношении для закона освещенности используются именно эти «нормали», т. е. фактически рассчитывается освещенность не плоской грани, а искривленной поверхности, что позволяет эффективно сгладить «граненую» структуру объекта. Сказанное выше поясняется рис.. Для каждой грани, помимо основной, истинной нормали п, рассчитываются три «нормали» п1, п2 n3. Каждая из них определяется как геометрическая сумма нормалей к граням, которым принадлежит данная вершина
Объем необходимых вычислений можно значительно сократить, если затенение Фонга выполнять с помощью так называемых карт затенения, подготовленных заранее (этот алгоритм предложил Майкл Абраш). Карта затенения представляет собой изображение плоской поверхности, освещаемой точечным источником света, расположенным над ее центром. Освещенность каждой точки этой карты рассчитывается на основе закона освещенности. Заметим, что точки карты, лежащие на концентрических окружностях, имеют одинаковую освещенность, посколькудля них угол между нормалью к поверхности и направлением на источник света одинаков. Карта затенения используется в качестве шаблона, задающего распределение освещенности в пределах грани. 27. Вычисление освещённости. Обратная трассировка лучей. Идея метода. Достоинства и недостатки. Для изображения теней, зеркальных и преломляющих поверхностей используется метод трассировки лучей. Прямая трассировка лучей (источник-> точка объекта -> рецептор) Часто используется обратная трассировка лучей (рецептор-> точка объекта -> источник) 1) Определить, какая точка объекта соответствует пикселу-рецептору. 2) Отследить ход луча, вычисляя его интенсивность и окраску, расщепляя луч при необходимости. Т. о., создается дерево лучей. Прекращение вычисления: -Затухание луча (большой путь) -Поглощение луча плохо отражающей поверхностью - Попадание луча в источник - Уход луча за пределы сцены Вычисление построенного дерева лучей с корнем в рецепторе дает окраску пиксела. Диффузное отражение – много лучей – считается отдельно.
показатель преломления n = c/v > 1
28. Вычисление освещённости. Метод излучательности. Идея метода. Достоинства и недостатки.
|

 =
=  0 £ q£ p/2, 0 £ kd £ 1 (4.5)
0 £ q£ p/2, 0 £ kd £ 1 (4.5) В отличие от диффузного, зеркальное отражение является направленным. Для идеально отражающей поверхности угол отражения равен углу падения и отраженный луч R лежит в одной плоскости с направлением на источник света L и нормалью к поверхности N (уравнение Френеля), и если направление на наблюдателя S отлично от R, то отраженный луч не виден вовсе. Для реальных поверхностей интенсивность отраженного света максимальна вдоль R и убывает при увеличении отклонения от этого направления, что выражается приближенной эмпирической формулой, основанной на модели Фонга:
В отличие от диффузного, зеркальное отражение является направленным. Для идеально отражающей поверхности угол отражения равен углу падения и отраженный луч R лежит в одной плоскости с направлением на источник света L и нормалью к поверхности N (уравнение Френеля), и если направление на наблюдателя S отлично от R, то отраженный луч не виден вовсе. Для реальных поверхностей интенсивность отраженного света максимальна вдоль R и убывает при увеличении отклонения от этого направления, что выражается приближенной эмпирической формулой, основанной на модели Фонга: =
=  , -p/2 £ a£ p/2, 0 £ ks £ 1 (4.6)
, -p/2 £ a£ p/2, 0 £ ks £ 1 (4.6)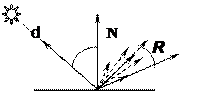
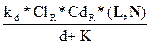 +
+  =
=


 Благодаря такому способу определения п1, п2 n3 каждая дополнительная «нормаль» является истинной нормалью к некоторой воображаемой выпуклой или вогнутой поверхности, проходящей через вершины граней (рис. 5.9, б). Далее, для каждой точки грани рассчитывается собственная «нормаль» как результат интерполяции «нормалей» по поверхности грани. Этот этап закраски по методу Фонга напоминает линейную интерполяцию освещенности по методу Гуро, однако в данном случае интерполируется не скалярная величина (освещенность), а вектор «нормали», задаваемый тремя координатами. По этой причине реализация затенения по методу Фонга требует значительных вычислительных затрат и редко используется в реальном масштабе времени.
Благодаря такому способу определения п1, п2 n3 каждая дополнительная «нормаль» является истинной нормалью к некоторой воображаемой выпуклой или вогнутой поверхности, проходящей через вершины граней (рис. 5.9, б). Далее, для каждой точки грани рассчитывается собственная «нормаль» как результат интерполяции «нормалей» по поверхности грани. Этот этап закраски по методу Фонга напоминает линейную интерполяцию освещенности по методу Гуро, однако в данном случае интерполируется не скалярная величина (освещенность), а вектор «нормали», задаваемый тремя координатами. По этой причине реализация затенения по методу Фонга требует значительных вычислительных затрат и редко используется в реальном масштабе времени. Преломление
Преломление Ход лучей света при преломлении на плоской поверхности, разделеляющей две прозрачные среды. Пунктиром обозначен отражённый луч. Угол преломления c больше угла падения j; это указывает, что в данном случае происходит преломление из оптически менее плотной 1-й среды в более оптически плотную 2-ю (n1<n2 ). п— нормаль к поверхности раздела(прозрачность 0 –нет, 1 – прозрачный).
Ход лучей света при преломлении на плоской поверхности, разделеляющей две прозрачные среды. Пунктиром обозначен отражённый луч. Угол преломления c больше угла падения j; это указывает, что в данном случае происходит преломление из оптически менее плотной 1-й среды в более оптически плотную 2-ю (n1<n2 ). п— нормаль к поверхности раздела(прозрачность 0 –нет, 1 – прозрачный).


