Как и кривые, поверхности в компьютерной графике обычно задаются параметрически. (1)  , где
, где  и
и  - независимые параметры.
- независимые параметры.
В матричной форме уравнение (1) записывается как
(2)  , где
, где  – множество точек в пространстве, образующих поверхность.
– множество точек в пространстве, образующих поверхность.
Как и в случае кривых, диапазон изменения параметров зависит от выбранного способа параметризации. При нормальной параметризации, т.е. при которой значения  и
и  нормированы, точка с координатами (
нормированы, точка с координатами ( ;
;  ) принадлежит единичному квадрату.
) принадлежит единичному квадрату.
 Если зафиксировать некоторое значение параметра
Если зафиксировать некоторое значение параметра 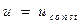 и изменять значение параметра
и изменять значение параметра  , то получится линия в пространстве, описываемая уравнением
, то получится линия в пространстве, описываемая уравнением  и называемая v -линией. Таким образом, набор фиксированных значений u порождает семейство v -линий. Аналогично определяются u -линии. Построив некоторое количество u -линий и v -линий, получим сетку топологически ортогональных параметрических кривых, каждая из которых принадлежит исходной поверхности. Параметры u и v являются внутренними криволинейными координатами на поверхности Q.
и называемая v -линией. Таким образом, набор фиксированных значений u порождает семейство v -линий. Аналогично определяются u -линии. Построив некоторое количество u -линий и v -линий, получим сетку топологически ортогональных параметрических кривых, каждая из которых принадлежит исходной поверхности. Параметры u и v являются внутренними криволинейными координатами на поверхности Q.
Поверхность Безье степени NxM задается выражением
(8)  , где
, где  ,
,  ,
,
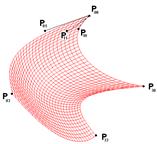 Для определения такой поверхность Безье требуется задать (N+1)x(M+1) точек. Чаще всего используются бикубические поверхности Безье (N=3, M=3), задаваемые 16-ю точками. Границами такого бикубического сегмента поверхности Безье являются кубические кривые Безье.
Для определения такой поверхность Безье требуется задать (N+1)x(M+1) точек. Чаще всего используются бикубические поверхности Безье (N=3, M=3), задаваемые 16-ю точками. Границами такого бикубического сегмента поверхности Безье являются кубические кривые Безье.
Подобно тому, как промежуточные управляющие точки кубической кривой задают направления касательных на ее концах, векторы  и
и  коллинеарны касательным к границам поверхности в точке
коллинеарны касательным к границам поверхности в точке  . Вектор
. Вектор  коллинеарен вектору кручения
коллинеарен вектору кручения  .
.

 , где
, где  и
и  - независимые параметры.
- независимые параметры. , где
, где  – множество точек в пространстве, образующих поверхность.
– множество точек в пространстве, образующих поверхность. Если зафиксировать некоторое значение параметра
Если зафиксировать некоторое значение параметра 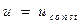 и изменять значение параметра
и изменять значение параметра  и называемая v -линией. Таким образом, набор фиксированных значений u порождает семейство v -линий. Аналогично определяются u -линии. Построив некоторое количество u -линий и v -линий, получим сетку топологически ортогональных параметрических кривых, каждая из которых принадлежит исходной поверхности. Параметры u и v являются внутренними криволинейными координатами на поверхности Q.
и называемая v -линией. Таким образом, набор фиксированных значений u порождает семейство v -линий. Аналогично определяются u -линии. Построив некоторое количество u -линий и v -линий, получим сетку топологически ортогональных параметрических кривых, каждая из которых принадлежит исходной поверхности. Параметры u и v являются внутренними криволинейными координатами на поверхности Q. , где
, где  ,
,  ,
, Для определения такой поверхность Безье требуется задать (N+1)x(M+1) точек. Чаще всего используются бикубические поверхности Безье (N=3, M=3), задаваемые 16-ю точками. Границами такого бикубического сегмента поверхности Безье являются кубические кривые Безье.
Для определения такой поверхность Безье требуется задать (N+1)x(M+1) точек. Чаще всего используются бикубические поверхности Безье (N=3, M=3), задаваемые 16-ю точками. Границами такого бикубического сегмента поверхности Безье являются кубические кривые Безье. и
и  коллинеарны касательным к границам поверхности в точке
коллинеарны касательным к границам поверхности в точке  . Вектор
. Вектор  коллинеарен вектору кручения
коллинеарен вектору кручения  .
.


