Линейчатая и бикубическая поверхности Кунса.
Линейчатую поверхность можно рассматривать как поверхность, получающуюся в результате пространственного движения отрезка прямой переменной длины. Сам отрезок в этом случае называются образующей линией, а траектории его концов – направляющими линиями. Можно также считать, что образующая линейно переводит точки одной направляющей линии в точки другой.
(5) где Параметрические линии линейчатой поверхности в одном направлении – отрезки, в другом – кривые, линейно трансформирующиеся от одной направляющей к другой. Билинейная поверхность является частным случаем линейчатой поверхности.
Для целей геометрического моделирования было бы более удобно задавать все четыре границы порции поверхности в виде кривых (6) Для “смешивания” граничных кривых можно использовать линейную интерполяцию: (7) Последний член вычитается, так как при сложении двух первых слагаемых, задающих интерполяцию в u и v направлениях возникает “лишняя” билинейная поверхность. Это происходит из-за того, что каждая из “угловых” точек принадлежит паре граничных кривых, например,
Линейчатая поверхность является частным случаем линейной поверхности Кунса.
|

 Линейчатая поверхность описывается уравнением:
Линейчатая поверхность описывается уравнением: ,
,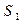 и
и  – граничные кривые, направляющие.
– граничные кривые, направляющие.
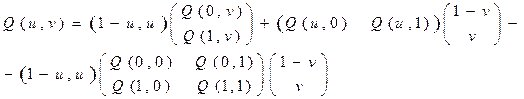
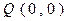 принадлежит одновременно кривым
принадлежит одновременно кривым  и
и  . Таким образом, при суммировании двух первых членов влияние каждой угловой точки удваивается.
. Таким образом, при суммировании двух первых членов влияние каждой угловой точки удваивается.



