Кусочное представление кривых кубическими сегментами. Идея метода. Достоинства и недостатки.
Известные из теории интерполяции многочлены Лагранжа отличаются наличием осцилляций и высокой степенью при большом количестве узлов (их степень, в общем случае, N-1, где N – число узлов). Высокая степень многочлена весьма нежелательна, так как она приводит к усложнению вычислений. На практике часто используются сплайны, т.е. кривые, составленные из сегментов, описываемых параметрически заданными многочленами третьей степени (кубическими) вида (1) Часто используется нормальная параметризация, при которой значение Рассмотрим, для начала, поведение одного кубического сегмента, заключенного между двумя соседними узлами интерполяции Pi(xi, yi) и Pi+1(xi+1, yi+1). Используя нормальную параметризацию, запишем условие, того, что сегмент кривой начинается в точке Pi(xi, yi) и заканчивается в точке Pi+1(xi+1, yi+1). (2) Очевидно, что для однозначного нахождения восьми неизвестных коэффициентов в уравнении (1) условий (2) недостаточно. Введем дополнительные условия, задав значения касательных векторов в начале и конце сегмента: (3) учитывая, что (4) Итак, мы имеем 8 уравнений (2) и (3) и восемь неизвестных в (1). Решая систему уравнений, находим неизвестные коэффициенты в (1).
|

 , где
, где 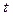 - независимый параметр
- независимый параметр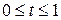 . Используется также, например, естественная параметризация, при которой значение
. Используется также, например, естественная параметризация, при которой значение  . Параметрическое представление удобно тем, что оно позволяет избежать “математических осложнений”, связанных с представлением в виде
. Параметрическое представление удобно тем, что оно позволяет избежать “математических осложнений”, связанных с представлением в виде 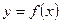 , например, кривых с самопересечениями.Третья степень многочлена обеспечивает удовлетворительное выполнение условий адекватной “плавности и приемлемой вычислительной трудоемкости.
, например, кривых с самопересечениями.Третья степень многочлена обеспечивает удовлетворительное выполнение условий адекватной “плавности и приемлемой вычислительной трудоемкости.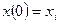 ;
; 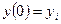 ;
; 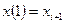 ;
; 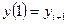 ;
; ;
; 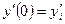 ;
;  ;
; 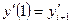 ,
, .
.


