Кривые Безье.
В общем случае, кривая Безье задается векторным уравнением (10) а Кривые Безье названы в честь предложившего их французского ученого П. Безье (Bezier). Кривые Безье обладают следующими свойствами: 1) Степень кривой N на единицу меньше числа вершин определяющего многогранника. Для двух точек кривая Безье превращается в отрезок прямой. 2) Начинается в точке 3) Вектор 4) Целиком лежит внутри выпуклой оболочки определяющего многоугольника.
Для нас наибольший интерес представляет частный случай кривой Безье – кривая Безье третьей степени (кубическая), создаваемая по четырем точкам. При N =3 выражение (10) примет вид: (11)
Кубические кривые Безье можно использовать в задачах сплайновой интерполяции для представления сегментов, если считать точки Для построения цепочки кубических сегментов Безье используется метод Graphics.DrawBeziers(Pen, Point[]). Для задания N сегментов требуется 4 + 3N точек, т.к. последняя точка любого внутреннего сегмента является первой следующего. Непрерывность касательной вдоль всего сплайна в этом методе не обеспечивается. Чтобы обеспечить непрерывность касательной, следует подбирать управляющие точки таким образом, чтобы каждый внутренний узел сплайна был серединой отрезка, соединяющего контрольную точку
|

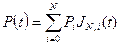 , где
, где 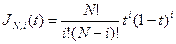 ,
, 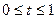 ,
,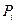 - вершины так называемого определяющего многоугольника.
- вершины так называемого определяющего многоугольника.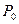 и заканчивается в точке
и заканчивается в точке  .
. сонаправлен с вектором касательной
сонаправлен с вектором касательной 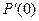 к кривой в ее начальной точке
к кривой в ее начальной точке 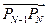 сонаправлен с вектором касательной
сонаправлен с вектором касательной 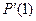 к кривой в ее конечной точке
к кривой в ее конечной точке 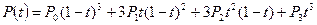 ,
, 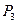 узлами интерполяционного сплайна, а точки
узлами интерполяционного сплайна, а точки 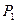 и
и 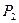 - управляющими точками сегмента.
- управляющими точками сегмента. предыдущего сегмента и контрольную точку
предыдущего сегмента и контрольную точку  следующего сегмента.
следующего сегмента.


