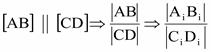Що означає вираз ?
а) [ ] якщо пряма (АВ) паралельна прямій (СD), то їх одноіменні проекції теж паралельні; b) [ ] проекції, одержані на паралельних площинах рівні між собою; c) [ ] відношення відрізків паралельних прямих дорівнює відношенню їх проекцій; d) [ ] при паралельному проеціюванні зберігається просте відношення довжин відрізків прямої. 19. Що означає вираз а) [ ] якщо пряма (АВ) паралельна прямый (СD), то їх одноіменні проекції теж паралельні; b) [ ] проекції, одержані на паралельних площинах рівні між собою; c) [ ] відношення відрізків паралельних прямих дорівнює відношенню їх проекцій; d) [ ] при паралельному проеціюванні зберігається просте відношення довжин відрізків прямої. 20. Що означає вираз а) [ ] якщо пряма (АВ) паралельна прямій (СD), то їх одноіменні проекції теж паралельні; b) [ ] проекції, одержані на паралельних площинах рівні між собою; c) [ ] відношення відрізків паралельних прямих дорівнює відношенню їх проекцій; d) [ ] при паралельному проеціюванні зберігається просте відношення довжин відрізків прямої. 21. Що означає вираз а) [ ] якщо пряма (АВ) паралельна прямій (СD), то їх одноіменні проекції теж паралельні; b) [ ] проекції, одержані на паралельних площинах рівні між собою; c) [ ] відношення відрізків паралельних прямих дорівнює відношенню їх проекцій; d) [ ] при паралельному проеціюванні зберігається просте відношення довжин відрізків прямої. 22. Що означає вираз а) [ ] якщо пряма (АВ) паралельна прямій (СD), то їх одноіменні проекції теж паралельні; b) [ ] проекції, одержані на паралельних площинах рівні між собою; c) [ ] відношення відрізків паралельних прямих дорівнює відношенню їх проекцій; d) [ ] довжина проекцій відрізка дорівнює довжині відрізка в просторі, помноженому на косинус кута, якого утворює відрізок з площиною проекцій. 23. Що означає вираз а) [ ] проекції, одержані на паралельних площинах рівні між собою; b) [ ] якщо одна сторона прямого кута паралельна площині проекції, то проекцією цього кута є прямий кут; c) [ ] відношення відрізків паралельних прямих дорівнює відношенню їх проекцій; d) [ ] довжина проекцій відрізка дорівнює довжині відрізка в просторі, помноженому на косинус кута якого утворює відрізок з площиною проекцій. 24. В нарисній геометрії вивчати способи побудови зображень геометричних форм за їх складовими елементами, починають з: а) [ ] точки; b) [ ] прямої; c) [ ] площини; d) [ ] геометричного тіла. 25. Що називають геометричною фігурою: а) [ ] довільну множину точок; b) [ ] довільну множину прямих; c) [ ] довільну множину площин; d) [ ] довільну множину відрізків. 26. Вкажіть геометричну фігуру: а) [ ] точка; b) [ ] відрізок; c) [ ] трикутник; d) [ ] пряма; 27. Побудова проекцій геометричних елементів ґрунтується на методі: а) [ ] координатному; b) [ ] проекціювання; c) [ ] аксонометрій; d) [ ] перспективи. 28. Перетин проекціювального променя з площиною проекцій дає проекцію: а) [ ] точки; b) [ ] прямої; c) [ ] площини; d) [ ] фігури. 29. Три взаємно перпендикулярні площини проекцій утворюють: а) [ ] три площини проекції; b) [ ] трьохгранний кут; c) [ ] двогранний кут; d) [ ] картинну площину. 30. Основними площинами проекцій є: а) [ ] горизонтальна та фронтальна; b) [ ] фронтальна та профільна; c) [ ] горизонтальна, фронтальна та загального положення; d) [ ] горизонтальна, фронтальна та профільна. 31. Яке взаємне розташування основних площин проекцій: а) [ ] паралельні між собою; b) [ ] суміщені з фронтальною площиною проекції; c) [ ] розташування залежить від напрямку проеціювання; d) [ ] взаємно перпендикулярні. 32. Яку з трьох площин проекцій вважають нерухомою: а) [ ] П1; b) [ ] П2; c) [ ] П3; d) [ ] горизонтальну.
|