1.  .
.
2. Функція не є ні парною, ні непарною. Функція неперіодична.
3. Оскільки функція неперервна на всій числовій осі, то вертикальних асимптот немає. Нахилені асимптоти теж є відсутніми, бо
 .
.
4. При 
 ; при
; при 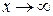
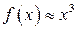 ;
;  .
.
5. Функція набуває нульового значення при  і
і  . Ці точки
. Ці точки
ділять числову вісь на три проміжки, в кожному з яких функція зберігає знак, точніше: на проміжку   , на проміжку , на проміжку   , а на проміжку , а на проміжку   .
Зробимо ескіз графіка функції (рис. 7.6).
Тепер виникає впевненість у тому, що функція .
Зробимо ескіз графіка функції (рис. 7.6).
Тепер виникає впевненість у тому, що функція
|  Рис. 7.6
Рис. 7.6
|
має дві екстремальні точки (одна з них  , а друга належить проміжку
, а друга належить проміжку  ) і одну точку перегину,
) і одну точку перегину,
6.  ;
;

 набуває нульового значення в точках
набуває нульового значення в точках  і
і  , які розбивають числову вісь на три проміжки.
, які розбивають числову вісь на три проміжки.
У проміжках  і
і  функція зростає, а в проміжку
функція зростає, а в проміжку  – спадає. Точка
– спадає. Точка  є точкою локального максимуму,
є точкою локального максимуму,  ; точка
; точка  є точкою локального мінімуму
є точкою локального мінімуму  .
.
 7.
7.  ;
;  набуває нульового значення в точці
набуває нульового значення в точці  , яка розбиває числову вісь на два проміжки.
, яка розбиває числову вісь на два проміжки.
На проміжку  функція опукла вгору, а на проміжку
функція опукла вгору, а на проміжку  –
–
вниз. Точка  є точкою перегину функції;
є точкою перегину функції;  .
.
На основі отриманих даних уточнюємо графік (рис. 7.7).
Приклад 7 Побудувати графік функції  . Розв’язання.1. . Розв’язання.1.  .
2. Функція не є ні парною, ні непарною.
Функція неперіодична. .
2. Функція не є ні парною, ні непарною.
Функція неперіодична.
|  Рис. 7.7
Рис. 7.7
|
3. Оскільки  є точкою розриву другого роду, то пряма
є точкою розриву другого роду, то пряма  буде вертикальною асимптотою графіка функції. Оскільки
буде вертикальною асимптотою графіка функції. Оскільки  при
при 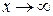 , то пряма
, то пряма 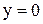 буде нахиленою (горизонтальною) асимптотою графіка функції.
буде нахиленою (горизонтальною) асимптотою графіка функції.
4.  .
.
5. При 
 , а при
, а при 
 .
.
і не існує при  :
:  . Цими точками числова вісь розділяється на три проміжки
. Цими точками числова вісь розділяється на три проміжки  ,
,  і
і  . У першому і третьому проміжку функція спадає, а в другому – зростає. Оскільки при
. У першому і третьому проміжку функція спадає, а в другому – зростає. Оскільки при  функція невизначена, то
функція невизначена, то  не є точкою екстремуму; в точці
не є точкою екстремуму; в точці  буде локальний максимум
буде локальний максимум  .
.
7.  ;
;  ,якщо
,якщо  ;
;  , якщо
, якщо  . Отже, точка
. Отже, точка 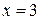 є точкою перегину функції
є точкою перегину функції  .
.
Отримані дані дозволяють уточнити ескіз графіка (рис. 7.9).
|
Рис. 7.9
| Приклад 8. Побудувати графік функції  .
Розв’язання.
1. .
Розв’язання.
1.  .
2. Функція не є ні парною, ні непарною, вона неперіодична. .
2. Функція не є ні парною, ні непарною, вона неперіодична.
|
3.  .
.
4. Пряма 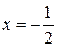 буде вертикальною асимптотою графіка функції (при цьому
буде вертикальною асимптотою графіка функції (при цьому  при
при  і
і  при
при  ), оскільки
), оскільки  при
при 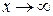 , то пряма
, то пряма  буде горизонтальною асимптотою графіка функції.
буде горизонтальною асимптотою графіка функції.
5. Зміна знака функції відбувається в точках  і
і  .
.
|
Побудуємо ескіз графіка (рис. 7.10).
6. 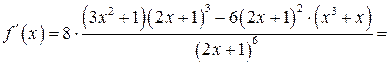
| 
|

 .
.
Отже, в точці  буде локальний максимум, що дорівнює
буде локальний максимум, що дорівнює  , а в точці
, а в точці  буде локальний мінімум, що дорівнює
буде локальний мінімум, що дорівнює  .
.
Можна зробити висновок про те, що ескіз графіка помилково відображає поведінку функції (рис. 7.11).
7.


 .
.

| У проміжках  і і  функція опукла вниз, а в проміжках функція опукла вниз, а в проміжках  , ,  – вгору. Точки – вгору. Точки  , ,  є точками перегину функції: є точками перегину функції:
 , ,  ; точка ; точка  не є точкою перегину, оскільки вона не входить до не є точкою перегину, оскільки вона не входить до  . .
|
Диагностическая работа по проверке сформированностиметапредметных умений у младших школьников
(2 класс)
Дата проведения: март, 2013 года.
Цель проведения: выявить уровень сформированностиметапредметных умений учащихся вторых классов
Инструкция к проведению
Учитель подписывает рабочие листы учащихся, указывая фамилию и имя полностью, школу, класс и УМК, по которому работает учитель.
Учащиеся могут выполнять работу в течение 2 – 3-х учебных дней по частям. Учитель читает инструкцию к заданию один раз. Ученики выбирают в каждом задании один предмет, познакомившись со всеми вариантами.Учитель не навязывает ученикам выбор предмета!
Учителем оценивается один вариант выполнения задания (на материале одного предмета)
Задание 1.
Цель:проверить сформированность умения планировать последовательность учебных действий в соответствии с поставленной задачей.


 .
. .
.
 ; при
; при 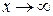
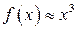 ;
;  .
. і
і  . Ці точки
. Ці точки
 , на проміжку
, на проміжку 

 .
Зробимо ескіз графіка функції (рис. 7.6).
Тепер виникає впевненість у тому, що функція
.
Зробимо ескіз графіка функції (рис. 7.6).
Тепер виникає впевненість у тому, що функція
 Рис. 7.6
Рис. 7.6
 ;
;
 набуває нульового значення в точках
набуває нульового значення в точках  і
і  , які розбивають числову вісь на три проміжки.
, які розбивають числову вісь на три проміжки. функція зростає, а в проміжку
функція зростає, а в проміжку  – спадає. Точка
– спадає. Точка  є точкою локального мінімуму
є точкою локального мінімуму  .
. 7.
7.  ;
;  набуває нульового значення в точці
набуває нульового значення в точці  , яка розбиває числову вісь на два проміжки.
, яка розбиває числову вісь на два проміжки. функція опукла вгору, а на проміжку
функція опукла вгору, а на проміжку  –
– .
. . Розв’язання.1.
. Розв’язання.1.  .
2. Функція не є ні парною, ні непарною.
Функція неперіодична.
.
2. Функція не є ні парною, ні непарною.
Функція неперіодична.
 Рис. 7.7
Рис. 7.7
 при
при 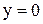 буде нахиленою (горизонтальною) асимптотою графіка функції.
буде нахиленою (горизонтальною) асимптотою графіка функції. .
.

 .
.

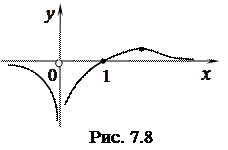
 . Цими точками числова вісь розділяється на три проміжки
. Цими точками числова вісь розділяється на три проміжки  і
і  . У першому і третьому проміжку функція спадає, а в другому – зростає. Оскільки при
. У першому і третьому проміжку функція спадає, а в другому – зростає. Оскільки при  .
. ;
;  ,якщо
,якщо  ;
;  , якщо
, якщо  . Отже, точка
. Отже, точка 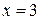 є точкою перегину функції
є точкою перегину функції  .
.
 .
Розв’язання.
1.
.
Розв’язання.
1.  .
2. Функція не є ні парною, ні непарною, вона неперіодична.
.
2. Функція не є ні парною, ні непарною, вона неперіодична.
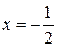 буде вертикальною асимптотою графіка функції (при цьому
буде вертикальною асимптотою графіка функції (при цьому  при
при  і
і  при
при  ), оскільки
), оскільки  при
при  буде горизонтальною асимптотою графіка функції.
буде горизонтальною асимптотою графіка функції. .
.
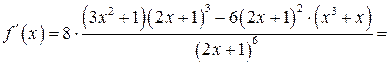


 .
. , а в точці
, а в точці  буде локальний мінімум, що дорівнює
буде локальний мінімум, що дорівнює  .
.
 .
.
 і
і  функція опукла вниз, а в проміжках
функція опукла вниз, а в проміжках  ,
,  ,
,  є точками перегину функції:
є точками перегину функції:
 ,
,  ; точка
; точка  не є точкою перегину, оскільки вона не входить до
не є точкою перегину, оскільки вона не входить до  .
.



