РЕШЕНИЕ ОБЩИХ ПРОБЛЕМ МНОЖЕСТВЕННОЙ РЕГРЕССИИ
И данные, и сама реальность не всегда подходят для построения концептуальной модели, лежащей в основе множественного регрессионного анализа. Связи не всегда линейны, в измерениях часто бывают ошибки и т.д. К счастью, математики -статистики предусмотрели некоторые пути к тому, чтобы приспособить множественную регрессию к урегулированию подобных проблем. Мы обсудим возможности решения трех из обычно возникающих проблем, с тем чтобы вы могли (1) понять, как преодолевать такие сложности в вашем конкретном случае применения множественной регрессии, и (2) получить представление о гибкости множественной регрессии как приема статистического анализа. Неинтервальные данные. В социальных науках важные переменные часто не могут быть измерены в интервальной шкале, нарушая, таким образом, условие об интервальном уровне измерения. Однако неинтервальные данные могут быть использованы в множественной регрессии при двух условиях. Во-первых, если измерение является дихотомией (или может быть преобразовано в нее), его можно использовать непосредственно для регрессии, попросту придав одному значению дихотомии код 1, а другому – 0. Например, в изучении международной торговли товары можно [c.447] классифицировать как “иностранные” и “отечественные”, приписав значению “иностранный” код 1, а значению “отечественный” – код 0. При регрессионном анализе такая схема будет восприниматься как интервальная, поскольку дихотомия имеет особые математические свойства. В результате мы можем интерпретировать частный коэффициент регрессии, посчитанный для любой закодированной дихотомически переменной, так же как мы сделали бы это в случае измерения по интервальной шкале. Неинтервальные переменные, которые имеют много категорий, могут быть приведены к виду, необходимому для множественной регрессии, путем использования системы фиктивных переменных. Рассмотрим, например, случай, где служебное положение измеряется только в категориях “высокое”, “среднее” и “низкое” в исследовании, целью которого является определение количества политических организаций, к которым принадлежит данный индивид, как функции образования (количества лет обучения) и служебного положения. Мы сможем использовать порядковые данные о профессии для множественной регрессии, если создадим две дихотомические фиктивные переменные, представляющие переменную “служебное положение”. Уравнение примет вид: Y' = а + b 1 X 1 + b 2 X 2 + b 3 X 3 +е, где Y’ – количество политических организаций, в которых состоит участник; Почему для выражения не интервальной переменной с тремя категориями используются только две фиктивные переменные? Потому что значения третьей фиктивной переменной будут точной линейной функцией двух других; таким образом, нарушится условие об отсутствии прямых мультиколлинеарных связей, и однозначный подсчет различных коэффициентов станет невозможным. [c.448] Когда бы ни использовался принцип создания фиктивных переменных, мы должны следовать правилу создания фиктивных переменных на одну меньше, чем имеется категорий в неинтервальной переменной. Судя по практике, рекомендуется обычно не брать ту категорию, в которой наименьшее количество случаев. В нашем примере фиктивная переменная не была представлена категорией “высокое служебное положение”, потому что должностей этого уровня очень мало. Значение частного коэффициента регрессии для этой исключенной градации подсчитывается путем решения уравнения регрессии. Так, в данном примере если в каком-либо случае переменная “служебное положение принимает значение “высокое”, то значения Х 1, X 2должны быть равны 0 и значение частного коэффициента регрессии для категории “высокое служебное положение” будет равно значению Q 5. Эффект взаимодействия. Обычно регрессия наименьших квадратов предполагает, что воздействие различных НП на ЗП независимы друг от друга и для выяснения общего влияния комплекса переменных можно их просто просуммировать. На практике же влияния одних переменных усиливают и дополняют эффект воздействия других. В любом случае, когда воздействие одной НП зависит от значения другой НП, существует эффект взаимодействия. Возвращаясь к примеру о выборах, приведенному выше, мы могли бы оспорить тот факт, что расходы на рекламу имеют различные результаты в случае уже пребывающих в должности (они обычно хорошо известны) и претендентов (им еще предстоит убедить избирателей в своей пригодности). Множественную регрессию можно приспособить к этой ситуации, если представить переменную “средства, вложенные в рекламу” (X 1) как результат взаимодействия между ней самой и занимаемым постом. Если мы предположим, что занимаемый пост представлен фиктивной переменной (Х 3), где претенденты имеют код 1, а занимающие посты – 0, новая регрессионная модель будет выглядеть так: Y' = а + b 1 X 1 + b 3(X 1 X 3) + b 2 X 2 + е, где Х 1 Х 3 – переменная взаимодействия, образованная произведением Х 1на Х 3. [c.449] Этот способ позволяет нам интерпретировать b 1 как однократный вклад расходов на рекламу в распределение голосования путем прекращения суммарного воздействия рекламы и должности на b 3 и получить таким образом более точные данные относительно значений Y. Мультиколлинеарность. Регрессионный анализ требует, чтобы ни одна независимая переменная не была четко скоррелирована с любой другой независимой переменной или с любой линейной комбинацией независимых переменных. Обычно соблюсти это строгое требование легко, поскольку в социальных науках редко бывает так, что значения одной переменной точно выводятся из известных значений другой или ряда других переменных. Однако многие важные переменные действительно тесно связаны друг с другом. (Возьмите урбанизацию и индустриализацию, образование и доход или партии и идеологию в Западной Европе.) Если корреляция между НП в регрессионной модели достаточно велика, подсчеты коэффициента будут неточными и мы не сможем доверять результатам регрессионного анализа. Значимая мультиколлинеарность может вызвать такие большие колебания в значении частного коэффициента регрессии, что сравнивать реальные воздействия различных НП на ЗП станет невозможно. Вдобавок коэффициенты могут не достичь статистической значимости даже в тех случаях, когда наблюдается существенная взаимосвязь, что ведет к неверной констатации отсутствия двумерной связи. Таким образом, очень важно, чтобы исследователи предпринимали серьезные попытки установить присутствие мультиколлинеарности и необходимые действия по ее корректировке. Мультиколлинеарность обычно определяют по одному или нескольким следующим признакам: 1. Высокий коэффициент R 2 в уравнении, но статистически незначимые коэффициенты регрессии (b). 2. Очень сильные колебания в значениях коэффициентов регрессии (b) для одной переменной, если из уравнения выводятся или вводятся в него другие НП. 3. Значения коэффициентов регрессии, которые значительно больше или меньше (как в абсолютных значениях, так и по отношению к коэффициентам других НП), чем можно ожидать, исходяиз теории и результатов других подобных исследований. [c.450] 4. Коэффициенты регрессии с неверным знаком, т.е. отрицательные тогда, когда у нас есть все основания ожидать положительного знака, и положительные тогда, когда есть основания ожидать отрицательного знака. Если хотя бы один из этих признаков появляется при регрессионном анализе, необходима проверка на мультиколлинеарность. Это делается путем регрессирования каждой НП на все другие НП. К примеру, мы хотим проверить уравнение Y’ = а + b 1 X 1 + b 2 X 2 + b 3 X 3 + е через такие уравнения: X 1 = а + b 2 X 2 + b 3 X 3 ; Если R2 для любого из этих уравнений будет выше, чем, скажем, 0,8, мы можем заключить, что имеется значимая мультиколлинеарность. Существует несколько способов корректировки мультиколлинеарности. Если у нас есть ряд добавочных по oотношению к выборке случаев (как, например, тогда, когда мы выбираем данные из опубликованного источника и можем просто обратиться к нему еще раз и сделать довыборку), увеличение размера выборки может в какой-то степени уменьшить мультиколлинеарность. Другой путь – определить, какие именно НП особенно тесно связаны друг с другом, и объединить их в единый фактор. Если, например, средства, вложенные в радио-, теле– и печатную рекламу, измеряются в нашем исследовании сенатских выборов отдельно, а мы обнаружим, что они тесно взаимосвязаны, можно объединить их в один признак услады в средства массовой информации, с тем чтобы уменьшить дестабилизирующее воздействие мультиколлинеарности. Естественно, любое подобное комбинирование будет работать только в том случае, если оно теоретически обосновано. Нельзя, к примеру, решать проблему мультиколлинеарности путем объединения занимаемого кандидатом поста и регионального расположения штата, поскольку теоретически они относятся к вещам, не связанным друг с другом. И наконец, можно попробовать справиться с мультиколлинеарностью, отбросив одну или [c.451] несколько тесно связанных переменных. Это может привести к искажениям, но, убирая сначала одну, потому другую из связанных НП и сравнивая результаты регрессий, можно по меньшей мере составить представление о том, какой урон наносят искажения, а какой – мультиколли-неарность. Сравнение независимых переменных. Всегда важно знать, какая из нескольких НП оказывает наибольшее влияние на зависимую переменную. Если бы мы хотели заставить людей, к примеру, пристегивать ремни, нам понадобилось бы, наверное, узнать, какие из факторов, способных вызвать такое поведение, могут сильнее всего повлиять на решение пристегиваться, и затем действовать наиболее эффективными методами. Анализ с применением множественной регрессии очень хорошо подходит для этого, поскольку предусматривает оценку влияния каждой отдельной НП на колебания ЗП одним из своих методов – частным коэффициентом регрессии. К сожалению, определение относительного влияния разных НП не тождественно простому сравнению их коэффициентов регрессии. В тех случаях, когда НП измеряются в разных единицах (количество долларов наряду с процентом избирателей, например), коэффициенты регрессии не отражают относительного воздействия НП на ЗП. Одним из возможных путей обойти это – стандартизировать переменные так, чтобы они были измерены в одних и тех же единицах, и снова произвести подсчеты коэффициента регрессии. Стандартизация измерений достигается путем преобразования числового ряда в единицы стандартного отклонения от значения среднего геометрического переменной посредством использования следующей формулы:
где звездочка означает, что переменная стандартизована; Когда числовые ряда заменены в уравнении регрессии на стандартизованные ряды, а выпадает, потому что стандартизация сводит его к 0, и уравнение приходит к общей формуле: Y’ = а + β; 1 X 1* + β; 2 X 2* + β; 3 X 3* +…+ β; n X n* + е, где β; представляет частный коэффициент стандартизованной регрессии и называется бета-вес, или бета-коэффициент. Вес корректирует частный нестандартизованный коэффициент регрессии путем деления стандартного отклонения НП на стандартное отклонение ЗП и может быть посчитан по формуле:
Бета-вес может быть интерпретирован как среднее изменение стандартного отклонения переменной Y, связанное с измерением стандартного отклонения переменной Х при постоянном воздействии других НП. Таким образом, β; со значением 0,5 означает, что изменение значения НП в одно стандартное отклонение вызовет изменение ЗП в половину стандартного отклонения. Таким образом, стандартизация позволяет сравнивать влияние нескольких независимых переменных внутри одного массива. Если же нам нужно выяснить взаимосвязи переменных между массивами, этот способ может ввести в заблуждение. Если, например, нам захочется изучить влияние количества вложенных средств на успех кандидатов на выборах в Соединенных Штатах и Мексике, мы обнаружим, что в распределении (а следовательно и в стандартном отклонении) ключевых переменных были существенные различия, поскольку организация кампании в средствах массовой информации в Соединенных Штатах стоит больше, и результаты выборов зависят от этого в одной стране больше, чем в другой. Поскольку значение β; является функцией вариации переменных (чем больше вариация, тем больше β; при прочих равных условиях), мы можем ошибаться, думая, что вложение средств дает в одной стране больший эффект, чем в другой, просто потому, что таковы математические обусловленные значения β;. Чтобы избежать такой ошибки, необходимо принять во внимание частный наклон [c.453] нестандатизованной регрессии в любом случае сравнения влияний НП в различных массивах, если вариация этой переменной значительно меняется от массива к массиву 6. [c.454] ПАТ-АНАЛИЗ* Регрессионный анализ может быть достаточно полезен для проверки отдельных гипотез и изучения относительного влияния различных независимых переменных. Однако регрессия предлагает такую модель причинных связей, которая не всегда отражает всю сложность окружающего мира. Если нам захочется определить решающие факторы расовой сегрегации в системе общеобразовательных школ, например, мы можем предположить, что школьная сегрегация вызвана сегрегацией в системе расселения (поскольку большинство школ тяготеет к географическим регионам), а она в свою очередь расовыми различиями в доходах. Диаграмма причин, или модель взаимосвязей, построенная по схеме, предложенной в гл. 2, изображена на модели 1. Модель1. X 1 – расовые различия в доходах, Х 2 – жилищная сегрегация и Х 3 – школьная сегрегация
Эта простая диаграмма – типичная модель, полученная в результате обычного регрессионного анализа; она показывает, что НП оказывают воздействие на ЗП независимо друг от друга. В реальной же социальной ситуации НП часто влияют друг на друга так же, как и на ЗП. Если вспомнить наш пример, то мало-мальские знания об объекте исследования позволят предположить, что различия в доходах влияют на жилищную сегрегацию так же, как и на школьную сегрегацию, поскольку менее дорогие и более дорогие дома обычно географически тяготеют друг к другу. Признание этого факта означало бы, что мы пересмотрели нашу модель, Можно предположить, что существует последовательное развитие, в [c.454] котором одна НП оказывает воздействие на ЗП исключительно через изменения, вызванные ею в другой НП. Это можно изобразить так:
|


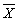 – значение среднего геометрического этой переменной для всех признаков;
– значение среднего геометрического этой переменной для всех признаков;




