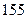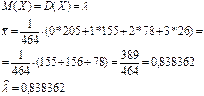162. Игральную кость бросили 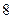 раз. При этом
раз. При этом 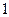 очко выпало
очко выпало 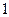 раз,
раз,  очка –
очка – 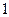 раз,
раз,  очка –
очка – 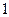 раз,
раз,  очка –
очка –  раза,
раза,  очков –
очков –  раза,
раза,  очков –
очков – 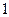 раз. Найдите эмпирическую функцию распределения числа очков, выпавших при бросании игральной кости.
раз. Найдите эмпирическую функцию распределения числа очков, выпавших при бросании игральной кости.
| Xi
| 1
| 2
| 3
| 4
| 5
| 6
|
| Ni
| 1
| 1
| 1
| 2
| 2
| 1
|
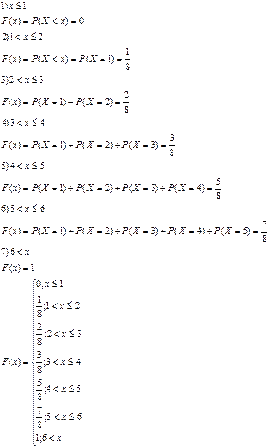
163. В четырех независимых испытаниях случайная величина  приняла следующие значения:
приняла следующие значения: 
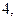

 Найдите несмещенную оценку дисперсии
Найдите несмещенную оценку дисперсии 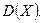
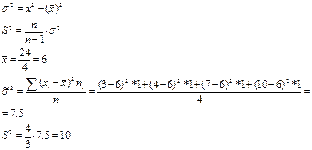
164. В  независимых испытаниях случайная величина
независимых испытаниях случайная величина  значениe
значениe  приняла
приняла  раз, а значение
раз, а значение  –
–  раз. Найдите несмещенную оценку дисперсии
раз. Найдите несмещенную оценку дисперсии 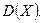
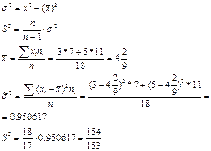
165. Даны результаты 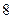 независимых измерений одной и той же величины прибором, не имеющим систематических ошибок:
независимых измерений одной и той же величины прибором, не имеющим систематических ошибок: 

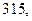
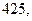
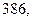
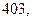

 м. Найдите несмещённую оценку дисперсии ошибок измерений, если истинная длина
м. Найдите несмещённую оценку дисперсии ошибок измерений, если истинная длина 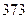 м.
м.
166. Даны результаты 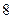 независимых измерений одной и той же величины прибором, не имеющим систематических ошибок:
независимых измерений одной и той же величины прибором, не имеющим систематических ошибок: 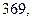

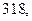



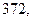
 м. Найдите несмещённую оценку дисперсии ошибок измерений, если истинная длина неизвестна.
м. Найдите несмещённую оценку дисперсии ошибок измерений, если истинная длина неизвестна.
167. Используя метод моментов, оцените параметры  и
и  равномерного распределения на отрезке
равномерного распределения на отрезке  по эмпирическому распределению
по эмпирическому распределению
Значение 
| 3
| 5
| 7
| 9
|
| Частота
| 21
| 18
| 15
| 26
|
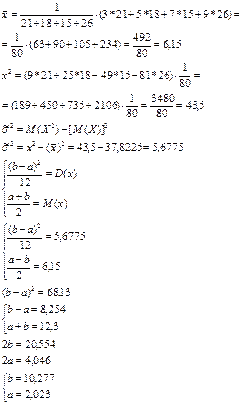
168. Случайная величина  (время бесперебойной работы устройства) имеет показательное распределение с плотностью
(время бесперебойной работы устройства) имеет показательное распределение с плотностью  (
(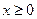 ). По эмпирическому распределению времени работы
). По эмпирическому распределению времени работы
| Время работы
| 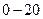
| 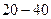
| 
| 
|
| Число устройств
| 
| 
| 
| 
|
методом моментов найдите точечную оценку  .
.
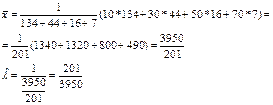
169. Случайная величина  распределена по закону Пуассона
распределена по закону Пуассона  . Результаты
. Результаты 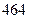 независимых наблюдений
независимых наблюдений  отражены в таблице
отражены в таблице
Найдите методом моментов точечную оценку  .
.
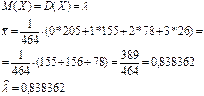

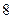 раз. При этом
раз. При этом  очко выпало
очко выпало  очка –
очка –  очка –
очка –  очка –
очка –  очков –
очков –  очков –
очков – 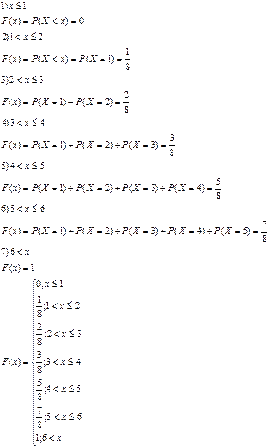
 приняла следующие значения:
приняла следующие значения: 
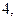

 Найдите несмещенную оценку дисперсии
Найдите несмещенную оценку дисперсии 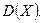
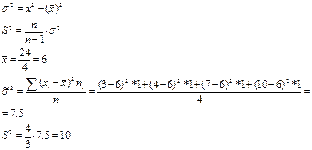
 независимых испытаниях случайная величина
независимых испытаниях случайная величина  раз, а значение
раз, а значение  раз. Найдите несмещенную оценку дисперсии
раз. Найдите несмещенную оценку дисперсии 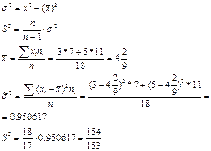


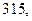
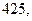
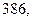
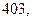

 м. Найдите несмещённую оценку дисперсии ошибок измерений, если истинная длина
м. Найдите несмещённую оценку дисперсии ошибок измерений, если истинная длина 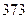 м.
м.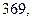




 м. Найдите несмещённую оценку дисперсии ошибок измерений, если истинная длина неизвестна.
м. Найдите несмещённую оценку дисперсии ошибок измерений, если истинная длина неизвестна. и
и  равномерного распределения на отрезке
равномерного распределения на отрезке  по эмпирическому распределению
по эмпирическому распределению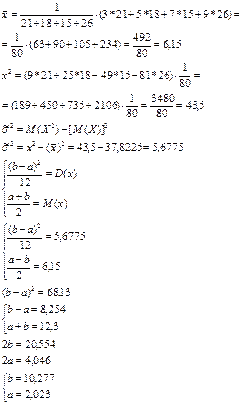
 (
(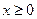 ). По эмпирическому распределению времени работы
). По эмпирическому распределению времени работы





 .
.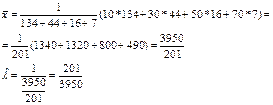
 . Результаты
. Результаты 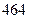 независимых наблюдений
независимых наблюдений